
��ͼ��������ABCD��������AEFG��һ��������A����G��E�ֱ����߶�AD��AB�ϣ�
��1������DF��BF������������AEFG�Ƶ�A��˳ʱ�뷽����ת���ж����⡰����ת�Ĺ����У��߶�DF��BF�ij�ʼ����ȡ��Ƿ���ȷ������ȷ����֤����������ȷ�������˵����
��2������������AEFG�Ƶ�A��˳ʱ�뷽����ת������DG������ת�����У����ܷ��ҵ�һ���߶εij����߶�DG�ij�ʼ����ȣ�����ͼΪ��˵�����ɣ�


��
�����㡿��ת�����ʣ�ȫ�������ε��ж������ʣ������ε����ʣ�
��ר�⡿����ͼ�����⣻�ۺ��⣮
����������1����Ȼ����A��F��B��ͬһֱ����ʱ��DF��BF��
��2��ע��ʹ�����������εıߺ�90��Ľǣ����жϳ���DAG�ա�BAE����ôDG=BE��
����𡿽⣺��1������ȷ��
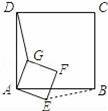
����������GAEF�Ƶ�A˳ʱ����ת45�㣬��ʱ��F�����߶�AB��AB���ӳ����ϣ�����������GAEF�Ƶ�A˳ʱ����ת��ʹ�õ�F�����߶�AB��AB���ӳ����ϣ�����ͼ��
��AD=a��AG=b��
��DF=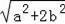
 ��a��
��a��
BF=|AB��AF|=|a��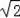
 b|��a��
b|��a��
��DF��BF������ʱDF��BF��
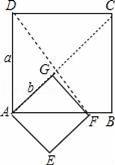
��2������BE���ɵá�ADG�ա�ABE��
��DG=BE����ͼ��
���ı���ABCD�������Σ�
��AD=AB��
���ı���GAEF�������Σ�
��AG=AE��
�֡ߡ�DAG+��GAB=90�㣬��BAE+��GAB=90�㣬
���DAG=��BAE��
���DAG�ա�BAE��
��DG=BE��


��������ע���������λ��ʱ���õ��Ĺ�ϵ���жϱ���ȣ�ͨ��Ҫ��ȫ�������Σ�
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
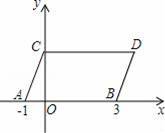
��ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ����1��0������3��0������ͬʱ����A��B�ֱ�����ƽ��2����λ��������ƽ��1����λ���ֱ�õ���A��B �Ķ�Ӧ��C��D������AC��BD��CD��
��1�����C��D�����꼰�ı���ABDC�����S�ı���ABDC��
��2����y�����Ƿ����һ��P������PA��PB��ʹS��PAB=S�ı���ABDC������������һ�㣬�����P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��a��b����cΪʵ���������и�ʽ��
��ac��bc����ac��bc����ac2��bc2����ac2��bc2����
 ��
��

���У���ȷ���У�������
A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
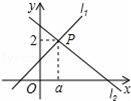
ֱ��l1��y=x+1��ֱ��l2��y=mx+n�ཻ�ڵ�P��a��2���������x�IJ���ʽx+1��mx+n�Ľ⼯Ϊ��������������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com