
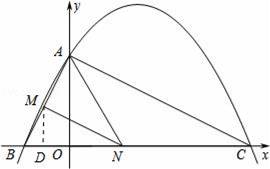
如图,已知二次函数y=ax2+
 x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+
 x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请直接写出此时点N的坐标;
(4)若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
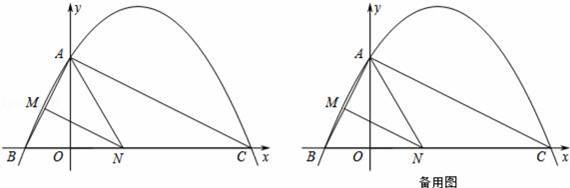

【考点】二次函数综合题.
【专题】压轴题.
【分析】(1)根据待定系数法即可求得;
(2)根据抛物线的解析式求得B的坐标,然后根据勾股定理分别求得AB2=20,AC2=80,BC10,然后根据勾股定理的逆定理即可证得△ABC是直角三角形.
(3)分别以A、C两点为圆心,AC长为半径画弧,与x轴交于三个点,由AC的垂直平分线与x轴交于一个点,即可求得点N的坐标;
(4)设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,根据三角形相似对应边成比例求得MD=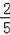
 (n+2),然后根据S△AMN=S△ABN﹣S△BMN
(n+2),然后根据S△AMN=S△ABN﹣S△BMN
得出关于n的二次函数,根据函数解析式求得即可.
【解答】解:(1)∵二次函数y=ax2+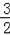
 x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),
x+c的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),
∴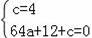
 ,
,
解得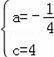
 .
.
∴抛物线表达式:y=﹣
 x2+
x2+
 x+4;
x+4;
(2)△ABC是直角三角形.
令y=0,则﹣
 x2+
x2+
 x+4=0,
x+4=0,
解得x1=8,x2=﹣2,
∴点B的坐标为(﹣2,0),
由已知可得,
在Rt△ABO中AB2=BO2+AO2=22+42=20,
在Rt△AOC中AC2=AO2+CO2=42+82=80,
又∵BC=OB+OC=2+8=10,
∴在△ABC中AB2+AC2=20+80=102=BC2
∴△ABC是直角三角形.
(3)∵A(0,4),C(8,0),
∴AC=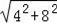
 =4
=4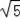
 ,
,
①以A为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(﹣8,0),
②以C为圆心,以AC长为半径作圆,交x轴于N,此时N的坐标为(8﹣4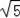
 ,0)或(8+4
,0)或(8+4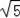
 ,0)
,0)
③作AC的垂直平分线,交x轴于N,此时N的坐标为(3,0),
综上,若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,点N的坐标分别为(﹣8,0)、(8﹣4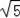
 ,0)、(3,0)、(8+4
,0)、(3,0)、(8+4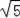
 ,0).
,0).
(4)设点N的坐标为(n,0),则BN=n+2,过M点作MD⊥x轴于点D,
∴MD∥OA,
∴△BMD∽△BAO,
∴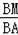
 =
=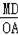
 ,
,
∵MN∥AC
∴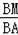
 =
=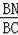
 ,
,
∴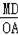
 =
=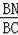
 ,
,
∵OA=4,BC=10,BN=n+2
∴MD=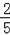
 (n+2),
(n+2),
∵S△AMN=S△ABN﹣S△BMN
=
 BN•OA﹣
BN•OA﹣
 BN•MD
BN•MD
=
 (n+2)×4﹣
(n+2)×4﹣
 ×
×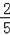
 (n+2)2
(n+2)2
=﹣
 (n﹣3)2+5,
(n﹣3)2+5,
∴当△AMN面积最大时,N点坐标为(3,0).

【点评】本题是二次函数的综合题,考查了待定系数法求解析式,勾股定理和逆定理,等腰三角形


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
在一个不透明的盒子中装有3个红球、2个黄球和1个绿球,这些球除了颜色外无其他差别.从中随机摸出一个小球,恰好是黄球的概率为( )
A.
 B.
B.
 C.
C.
 D.
D.

查看答案和解析>>
科目:初中数学 来源: 题型:
甲盒装有3个乒乓球,分别标号为1,2,3;乙盒装有2个乒乓球,分别标号为1,2.现分别从每个盒中随机地取出1个球,则取出的两球标号之和为4的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com