
【题目】定义:如果一个四边形的一组对角互余,那么我们称这个四边形为“对角互余四边形”.

(1)如图①,在对角互余四边形ABCD中,∠B=60°,且AC⊥BC,AC⊥AD,若BC=1,则四边形ABCD的面积为 ;
(2)如图②,在对角互余四边形ABCD中,AB=BC,BD=13,∠ABC+∠ADC=90°,AD=8,CD=6,求四边形ABCD的面积;
(3)如图③,在△ABC中,BC=2AB,∠ABC=60°,以AC为边在△ABC异侧作△ACD,且∠ADC=30°,若BD=10,CD=6,求△ACD的面积.
【答案】(1)2![]() ;(2)36;(3)
;(2)36;(3)![]() .
.
【解析】
(1)由AC⊥BC,AC⊥AD,得出∠ACB=∠CAD=90°,利用含30°直角三角形三边的特殊关系以及勾股定理,就可以解决问题;
(2)将△BAD绕点B顺时针旋转到△BCE,则△BCE≌△BAD,连接DE,作BH⊥DE于H,作CG⊥DE于G,作CF⊥BH于F.这样可以求∠DCE=90°,则可以得到DE的长,进而把四边形ABCD的面积转化为△BCD和△BCE的面积之和,△BDE和△CDE的面积容易算出来,则四边形ABCD面积可求;
(3)取BC的中点E,连接AE,作CF⊥AD于F,DG⊥BC于G,则BE=CE=![]() BC,证出△ABE是等边三角形,得出∠BAE=∠AEB=60°,AE=BE=CE,得出∠EAC=∠ECA= =30°,证出∠BAC=∠BAE+∠EAC=90°,得出AC=
BC,证出△ABE是等边三角形,得出∠BAE=∠AEB=60°,AE=BE=CE,得出∠EAC=∠ECA= =30°,证出∠BAC=∠BAE+∠EAC=90°,得出AC=![]() AB,设AB=x,则AC=
AB,设AB=x,则AC=![]() x,由直角三角形的性质得出CF=3,从而DF=3
x,由直角三角形的性质得出CF=3,从而DF=3![]() ,设CG=a,AF=y,证明△ACF∽△CDG,得出
,设CG=a,AF=y,证明△ACF∽△CDG,得出![]() ,求出y=
,求出y=![]() ,由勾股定理得出y2=(
,由勾股定理得出y2=(![]() x)2-32=3x2-9,b2=62-a2=102-(2x+a)2,(2x+a)2+b2=132,整理得出a=
x)2-32=3x2-9,b2=62-a2=102-(2x+a)2,(2x+a)2+b2=132,整理得出a=![]() ,进而得y=
,进而得y=![]() ,得出[
,得出[![]() ]2=3x2-9,解得x2=34-6
]2=3x2-9,解得x2=34-6![]() ,得出y2=(
,得出y2=(![]() )2,解得y=
)2,解得y=![]() -3
-3![]() ,得出AD=AF+DF=
,得出AD=AF+DF=![]() ,由三角形面积即可得出答案.
,由三角形面积即可得出答案.
解:(1)∵AC⊥BC,AC⊥AD,
∴∠ACB=∠CAD=90°,
∵对角互余四边形ABCD中,∠B=60°,
∴∠D=30°,
在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,
∴∠BAC=30°,
∴AB=2BC=2,AC=![]() BC=
BC=![]() ,
,
在Rt△ACD中,∠CAD=90°,∠D=30°,
∴AD=![]() AC=3,CD=2AC=2
AC=3,CD=2AC=2![]() ,
,
∵S△ABC=![]() ACBC=
ACBC=![]() ×
×![]() ×1=
×1=![]() ,
,
S△ACD═![]() ACAD=
ACAD=![]() ×
×![]() ×3=
×3=![]() ,
,
∴S四边形ABCD=S△ABC+S△ACD=2![]() ,
,
故答案为:2![]() ;
;
(2)将△BAD绕点B顺时针旋转到△BCE,如图②所示:
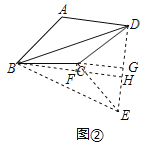
则△BCE≌△BAD,
连接DE,作BH⊥DE于H,作CG⊥DE于G,作CF⊥BH于F.
∴∠CFH=∠FHG=∠HGC=90°,
∴四边形CFHG是矩形,
∴FH=CG,CF=HG,
∵△BCE≌△BAD,
∴BE=BD=13,∠CBE=∠ABD,∠CEB=∠ADB,CE=AD=8,
∵∠ABC+∠ADC=90°,
∴∠DBC+∠CBE+∠BDC+∠CEB=90°,
∴∠CDE+∠CED=90°,
∴∠DCE=90°,
在△BDE中,根据勾股定理可得:DE=![]() =
=![]() =10,
=10,
∵BD=BE,BH⊥DE,
∴EH=DH=5,
∴BH=![]() =
=![]() =12,
=12,
∴S△BED=![]() BHDE=
BHDE=![]() ×12×10=60,
×12×10=60,
S△CED=![]() CDCE=
CDCE=![]() ×6×8=24,
×6×8=24,
∵△BCE≌△BAD,
∴S四边形ABCD=S△BCD+S△BCE=S△BED﹣S△CED=60﹣24=36;
(3)取BC的中点E,连接AE,作CF⊥AD于F,DG⊥BC于G,如图③所示:
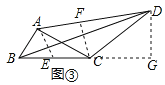
则BE=CE=![]() BC,
BC,
∵BC=2AB,
∴AB=BE,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴∠BAE=∠AEB=60°,AE=BE=CE,
∴∠EAC=∠ECA=![]() ∠AEB=30°,
∠AEB=30°,
∴∠BAC=∠BAE+∠EAC=90°,
∴AC=![]() AB,
AB,
设AB=x,则AC=![]() x,
x,
∵∠ADC=30°,
∴CF=![]() CD=3,DF=
CD=3,DF=![]() CF=3
CF=3![]() ,
,
设CG=a,AF=y,
在四边形ABCD中,∠ABC+∠BCD+∠ADC+∠BAC+∠DAC=360°,
∴∠DAC+∠BCD=180°,
∵∠BCD+∠DCG=180°,
∴∠DAC=∠DCG,
∵∠AFC=∠CGD=90°,
∴△ACF∽△CDG,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴y![]() ,
,
在Rt△ACF中,Rt△CDG和Rt△BDG中,由勾股定理得:y2=(![]() x)2﹣32=3x2﹣9,b2=62﹣a2=102﹣(2x+a)2,(2x+a)2+b2=132,
x)2﹣32=3x2﹣9,b2=62﹣a2=102﹣(2x+a)2,(2x+a)2+b2=132,
整理得:x2+ax﹣16=0,
∴a=![]() ,
,
∴y=![]() =
=![]() ×
×![]() =
=![]() ,
,
∴[![]() ]2=3x2﹣9,
]2=3x2﹣9,
整理得:x4﹣68x2+364=0,
解得:x2=34﹣6![]() ,或x2=34+6
,或x2=34+6![]() (不合题意舍去),
(不合题意舍去),
∴x2=34﹣6![]() ,
,
∴y2=3(34﹣6![]() )﹣9=93﹣18
)﹣9=93﹣18![]() =93﹣2
=93﹣2![]() =(
=(![]() )2,
)2,
∴y=![]() ﹣3
﹣3![]() ,
,
∴AF=![]() ﹣3
﹣3![]() ,
,
∴AD=AF+DF=![]() ,
,
∴△ACD的面积=![]() AD×CF=
AD×CF=![]() ×
×![]() ×3=
×3=![]() .
.


科目:初中数学 来源: 题型:
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在斜边
在斜边![]() 上(
上(![]() ),作
),作![]() ,且
,且![]() ,连接
,连接![]() ,如图(1).
,如图(1).
(1)求证:![]() ;
;
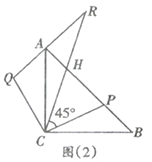
(2)延长![]() 至点
至点![]() ,使得
,使得![]() ,
,![]() 与
与![]() 交于点
交于点![]() .如图(2).
.如图(2).
①求证:![]() ;
;
②求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
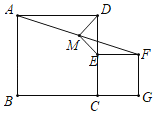
【题目】如图,已知正方形ABCD与正方形CEFG,点E在CD上,点G在BC的延长线上,M是AF的中点,连接DM,EM.
(1)填空:DM与EM数量关系和位置关系为 (直接填写);
(2)若AB=4,设CE=x(0<x<4),△MEF面积为y,求y关于x的函数关系式[可利用(1)的结论],并求出y的最大值;
(3)如果将正方形CEFG绕点C顺时针旋转任意角度,我们发现DM与EM数量关系与位置关系仍未发生改变.
①若正方形ABCD边长AB=13,正方形CEFG边长CE=5,当D,E,F三点旋转至同一条直线上时,求出MF的长;
②证明结论:正方形CEFG绕点C顺时针旋转任意角度,DM与EM数量关系与位置关系仍未发生改变.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:在一次聚会上,规定每两个人见面必须握手,且只握手1次.
(1)若参加聚会的人数为3,则共握手___次;若参加聚会的人数为5,则共握手___次;
(2)若参加聚会的人数为![]() (
(![]() 为正整数),则共握手___次;
为正整数),则共握手___次;
(3)若参加聚会的人共握手28次,请求出参加聚会的人数.
拓展:嘉嘉给琪琪出题:“若线段![]() 上共有
上共有![]() 个点(含端点
个点(含端点![]() ,
,![]() ),线段总数为30,求
),线段总数为30,求![]() 的值.”
的值.”
琪琪的思考:“在这个问题上,线段总数不可能为30.”琪琪的思考对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解本校九年级男生“引体向上”项目的训练情况,随机抽取该年级部分男生进行了一次测试(满分15分,成绩均记为整数分),并按测试成绩(单位:分)分成四类:A类(12≤m≤15),B类(9≤m≤11),C类(6≤m≤8),D类(m≤5)绘制出以下两幅不完整的统汁图,请根据图中信息解答下列问题:
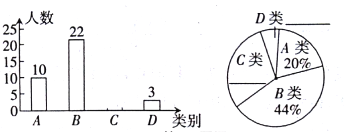
(l)本次抽取样本容量为____,扇形统计图中A类所对的圆心角是____度;
(2)请补全统计图;
(3)若该校九年级男生有300名,请估计该校九年级男生“引体向上”项目成绩为C类的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆
(辆![]() 小时)指单位时间内通过道路指定断面的车辆数;速度
小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米
(千米![]() 小时)指通过道路指定断面的车辆速度,密度
小时)指通过道路指定断面的车辆速度,密度![]() (辆
(辆![]() 千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量
千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度v(千米/小时) |
|
|
|
|
|
|
|
|
流量q(辆/小时) |
|
|
|
|
|
|
|
|
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确是_____________________.(只填上正确答案的序号)
关系最准确是_____________________.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() ,
,![]() ,
,![]() 满足
满足![]() ,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当
,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵?
在什么范围时,该路段将出现轻度拥堵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,若二次函数
,若二次函数![]() 的图象过
的图象过![]() 两点,且该函数图象的顶点为
两点,且该函数图象的顶点为![]() ,其中
,其中![]() ,
,![]() 是整数,且
是整数,且![]() ,
,![]() ,则
,则![]() 的值为__________.
的值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据北京市统计局发布的统计数据显示,北京市近五年国民生产总值数据如图1所示,2017年国民生产总值中第一产业、第二产业、第三产业所占比例如图2所示,根据以上信息,下列判断错误的是( )
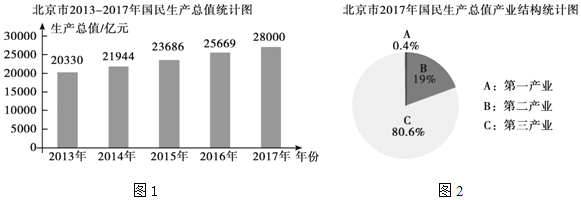
A.2013年至2017年北京市国民生产总值逐年增加
B.2017年第二产业生产总值为5 320亿元
C.2017年比2016年的国民生产总值增加了10%
D.若从2018年开始,每一年的国民生产总值比前一年均增长10%,到2019年的国民生产总值将达到33 880亿元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班共30名同学参加了网络上第二课堂的禁毒知识竞赛(共20道选择题),学习委员对竞赛结果进行了统计,发现每个人答题正确题数都超过15题.通过统计制成了下表,结合表中信息,解答下列问题:
答对题数 | 16 | 17 | 18 | 19 | 20 |
人数 | 3 | 9 | 6 | 4 |
(1)补统计表中数据:
(2)求这30名同学答对题目的平均数、众数和中位数;
(3)答题正确率为100%的4名同学中恰好是2名男同学和2名女同学,现从中随机抽取2名同学参加学校禁毒知识抢答大赛,问抽到1男1女的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com