
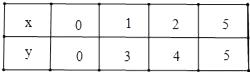
ЁОЬтФПЁПШчЭМЃЌЧНУцOCгыЕиУцODДЙжБЃЌвЛМмЬнзгABГЄ5УзЃЌПЊЪМЪБЬнзгНєЬљЧНУцЃЌЬнзгЖЅЖЫAбиЧНУцдШЫйУПЗжжгЯђЯТЛЌЖЏ1УзЃЌxЗжжгКѓЕуAЛЌЖЏЕНЕуAЁфЃЌЬнзгЕзЖЫBбиЕиУцЯђзѓЛЌЖЏЕНЕуBЁфЃЌOBЁф=yУзЃЌЛЌЖЏЪБЬнзгГЄЖШБЃГжВЛБфЃЎ
ЃЈ1ЃЉЕБx=1ЪБЃЌy=УзЃЛ
ЃЈ2ЃЉЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉбаОПЃЈ2ЃЉжаКЏЪ§ЭМЯѓМАЦфаджЪЃЎ
ЂйЬюаДЯТБэЃЌВЂдкЫљИјЕФзјБъЯЕжаЛГіКЏЪ§ЭМЯѓЃЛ
ЂкШчЙћЕуPЃЈxЃЌyЃЉдкЃЈ2ЃЉжаЕФКЏЪ§ЭМЯѓЩЯЃЌЧѓжЄЃКЕуPЕНЕуQЃЈ5ЃЌ0ЃЉЕФОрРыЪЧЖЈжЕЃЛ
ЃЈ4ЃЉЬнзгЕзЖЫBбиЕиУцЯђзѓЛЌЖЏЕФЫйЖШЪЧ
A.дШЫй
B.МгЫй
C.МѕЫй
D.ЯШМѕЫйКѓМгЫйЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉ3
ЃЈ2ЃЉНтЃК ![]() ЃЌЃЈ0ЁмxЁм5ЃЉ
ЃЌЃЈ0ЁмxЁм5ЃЉ
ЃЈ3ЃЉНтЃКЂйЬюБэЃК
ЂкЭМЯѓШчЭМЫљЪОЃК
Ёп ![]() ЃЌ
ЃЌ
Ёрy2+ЃЈ5ЉxЃЉ2=52ЃЌ
МДPQ2=PR2+RQ2=25ЃЌ
ЁрPQ=5ЃЌ
ЁрPЕНЕуQЃЈ5ЃЌ0ЃЉЕФОрРыЪЧЖЈжЕ
ЃЈ4ЃЉC
ЁОНтЮіЁПЃЈ1ЃЉx=1ЪБЃЌAЁфB=5Љ1=4ЃЌAЁфBЁф=5ЃЌ
ЁпЁЯO=90ЁуЃЌ
Ёрy=OBЁф= ![]() =3ЃЎ
=3ЃЎ
ЫљвдД№АИЪЧ3ЃЎ
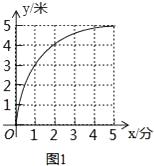
гЩЃЈ4ЃЉгыЃЈ3ЃЉПЩжЊЃЌКЏЪ§ЭМЯѓЪЧвдQЮЊдВаФЕФдВЛЁЃЌ
ШчЭМ2жаЃЌдкАыОЖOQЩЯШЁAB=BCЃЌЙ§AЁЂBЁЂCзїxжсЕФДЙЯпНЛдВЛЁгкDЁЂEЁЂFЃЌзїDMЁЭBEЃЌENЁЭCFЃЌбгГЄDEНЛCFгкGЃЎФЧУДGN=EMЃЌ
ЁпGNЃОFNЃЌ
ЁрEMЃОFNЃЌ
МДЕуAвЦЖЏЕФОрРыДѓгкЕуBвЦЖЏЕФОрРыЃЌ
ЁрЪЧМѕЫйЃЌ
ЫљвдД№АИЪЧЃКCЃЎ
ЁОПМЕуОЋЮіЁПНтД№ДЫЬтЕФЙиМќдкгкРэНтСНЕуМфЕФОрРыЕФЯрЙижЊЪЖЃЌеЦЮеЭЌжсСНЕуЧѓОрРыЃЌДѓМѕаЁЪ§ОЭЮЊжЎЃЎгыжсЕШОрСНИіЕуЃЌМфОрЧѓЗЈврШчДЫЃЎЦНУцШЮвтСНИіЕуЃЌКсзнБъВюЯШЧѓжЕЃЎВюЗНЯрМгПЊЦНЗНЃЌОрРыЙЋЪНвЊРЮМЧЃЌвдМАЖдОиаЮЕФаджЪЕФРэНтЃЌСЫНтОиаЮЕФЫФИіНЧЖМЪЧжБНЧЃЌОиаЮЕФЖдНЧЯпЯрЕШЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABCDЕФЖдНЧЯпACЁЂBDНЛгкЕуOЃЌAEЦНЗжЁЯBADНЛBCгкЕуEЃЌЧвЁЯADC=60ЁуЃЌAB=![]() BCЃЌСЌНгOEЃЎЯТСаНсТлЃКЂйЁЯCAD=30ЁуЃЛЂкSABCD=ABACЃЛЂлOB=ABЃЛЂмOE=
BCЃЌСЌНгOEЃЎЯТСаНсТлЃКЂйЁЯCAD=30ЁуЃЛЂкSABCD=ABACЃЛЂлOB=ABЃЛЂмOE=![]() BCЃЌГЩСЂЕФИіЪ§гаЃЈЁЁЁЁЃЉ
BCЃЌГЩСЂЕФИіЪ§гаЃЈЁЁЁЁЃЉ

A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕШБпЁїABCжаЃЌЕуHдкБпBCЩЯЃЌЕуKдкБпACЩЯЃЌЧвТњзуAK=HCЃЌСЌНгAHЁЂBKНЛгкЕуF.
(1)ШчЭМ1ЃЌЧѓЁЯAFBЕФЖШЪ§ЃЛ
(2)ШчЭМ2ЃЌСЌНгFCЃЌШєЁЯBFC=90ЁуЃЌЕуGЮЊБп ACЩЯвЛЕуЃЌЧвТњзуЁЯGFC=30ЁуЃЌЧѓжЄЃКAGЁЭBG
(3)ШчЭМ3ЃЌдк(2)ЬѕМўЯТЃЌдкBFЩЯШЁDЪЙЕУDF=AFЃЌСЌНгCDНЛAHгкEЃЌШєЁїDEFУцЛ§ЮЊ1ЃЌ дђЁїAHCЕФУцЛ§ЮЊ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊ![]() ЃЌ
ЃЌ![]() КЭ
КЭ![]() ЕФЦНЗжЯпЯрНЛгк
ЕФЦНЗжЯпЯрНЛгк![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФЖШЪ§ЮЊЃЈ ЃЉ
ЕФЖШЪ§ЮЊЃЈ ЃЉ

A.100ЁуB.130ЁуC.140ЁуD.160Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИљОнЬтвтЭъГЩЯТСаЭЦРэЙ§ГЬЃК
вбжЊЃКШчЭМЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌДЙзуЗжБ№ЮЊ
ЃЌДЙзуЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ![]() ЃЎЧѓжЄЃК
ЃЎЧѓжЄЃК![]() ЃЎ
ЃЎ

жЄУїЃК![]() ЃЌ
ЃЌ![]() ЃЈвбжЊЃЉ
ЃЈвбжЊЃЉ
![]() ЃЈДЙжБЕФЖЈвхЃЉ
ЃЈДЙжБЕФЖЈвхЃЉ
![]() ЃЈ__________ЃЉ
ЃЈ__________ЃЉ
![]() __________ЃЈ__________ЃЉ
__________ЃЈ__________ЃЉ
гж![]() ЃЈвбжЊЃЉ
ЃЈвбжЊЃЉ
![]() __________
__________![]() ЃЈ__________ЃЉ
ЃЈ__________ЃЉ
![]() ЃЈ__________ЃЉЃЎ
ЃЈ__________ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() гк
гк![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() НЛ
НЛ![]() гк
гк![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гк
гк![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЎ
ЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНЭЌбЇЕФМвгыбЇаЃЕФОрРыОљЮЊ3000УзЃЎМзЭЌбЇЯШВНаа600УзЃЌШЛКѓГЫЙЋНЛГЕШЅбЇаЃЁЂввЭЌбЇЦяздааГЕШЅбЇаЃЃЎвбжЊМзВНааЫйЖШЪЧввЦяздааГЕЫйЖШЕФ![]() ЃЌЙЋНЛГЕЕФЫйЖШЪЧввЦяздааГЕЫйЖШЕФ2БЖЃЎМзввСНЭЌбЇЭЌЪБДгМвЗЂШЅбЇаЃЃЌНсЙћМзЭЌбЇБШввЭЌбЇдчЕН2ЗжжгЃЎ
ЃЌЙЋНЛГЕЕФЫйЖШЪЧввЦяздааГЕЫйЖШЕФ2БЖЃЎМзввСНЭЌбЇЭЌЪБДгМвЗЂШЅбЇаЃЃЌНсЙћМзЭЌбЇБШввЭЌбЇдчЕН2ЗжжгЃЎ
ЃЈ1ЃЉЧѓввЦяздааГЕЕФЫйЖШЃЛ
ЃЈ2ЃЉЕБМзЕНДябЇаЃЪБЃЌввЭЌбЇРыбЇаЃЛЙгаЖрдЖЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
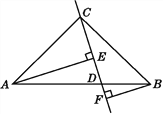
ЁОЬтФПЁПШчЭМЃКдкЁїABCжа,AC=BC,DЪЧABЩЯЕФвЛЕу,AEЁЭCDгкЕуE,BFЁЭCDгкЕуF,ШєCE=BF,AE=EF+BF.ЪдХаЖЯACгыBCЕФЮЛжУЙиЯЕ,ВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпaЃЌbБЛжБЯпcЃЌdЫљНиЃЌжБЯпaЃЌcЃЌdЯрНЛгкЕуOЃЌАДвЊЧѓЭъГЩЯТСаИїаЁЬтЃЎ
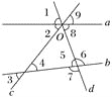
(1)дкЭМжаЕФЁЯ1ЁЋЁЯ9ет9ИіНЧжаЃЌЭЌЮЛНЧЙВгаЖрЩйЖдЃПЧыФуШЋВПаДГіРДЃЛ
(2)ЁЯ4КЭЁЯ5ЪЧЪВУДЮЛжУЙиЯЕЕФНЧЃПЁЯ6КЭЁЯ8жЎМфЕФЮЛжУЙиЯЕгыЁЯ4КЭЁЯ5ЕФЯрЭЌТ№ЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com