
【题目】如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC.
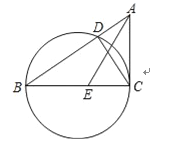
(1)求证:CA是圆的切线;
(2)若点E是BC上一点,已知BE=6,tan∠ABC=![]() ,tan∠AEC=
,tan∠AEC=![]() ,求圆的直径.
,求圆的直径.
【答案】(1)CA是圆的切线;(2)圆的直径是10.
【解析】
试题分析:(1)根据圆周角定理BC得到∠BDC=90°,推出∠ACD+∠DCB=90°,即BC⊥CA,即可判断CA是圆的切线;
(2)根据锐角三角函数的定义得到tan∠AEC=![]() ,tan∠ABC=
,tan∠ABC=![]() ,推出AC=
,推出AC=![]() EC,BC=
EC,BC=![]() AC,代入BC﹣EC=BE即可求出AC,进一步求出BC即可.
AC,代入BC﹣EC=BE即可求出AC,进一步求出BC即可.
试题解析:(1)证明:∵BC是直径,
∴∠BDC=90°,
∴∠ABC+∠DCB=90°,
∵∠ACD=∠ABC,
∴∠ACD+∠DCB=90°,
∴BC⊥CA,∴CA是圆的切线.
(2)解:在Rt△AEC中,tan∠AEC=![]() ,
,
∴![]() ,AC=
,AC=![]() EC,
EC,
在Rt△ABC中,tan∠ABC=![]() ,
,
∴![]() ,BC=
,BC=![]() AC,
AC,
∵BC﹣EC=BE,BE=6,
∴![]() ,
,
解得:![]() ,
,
∴BC=![]() =10,
=10,
答:圆的直径是10.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】若二次函数y=-(x-m)2+1,当x≤2时,y随x的增大而增大,则m的取值范围是( )
A. m=2 B. m>2 C. m≥2 D. m≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
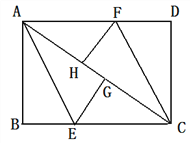
【题目】如图,在矩形ABCD中,AC是对角线,E、F分别在BC、AD边上,将边AB沿AE折叠,点B落在对角线AC上的G处,将边CD沿CF折叠,点D落在对角线AC上的点H处 .
(1)求证:四边形AECF是平行四边形.
(2)若AB=6,AC=10,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
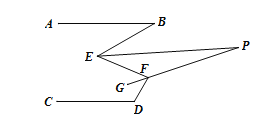
【题目】(10分)如图下图所示,已知AB//CD, ∠B=30°,∠D=120°;

(1)若∠E=60°,则∠E=______;
(2)请探索∠E与∠F之间满足的数量关系?说明理由.
(3)如下图所示,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=(m+1)x|2m|﹣1 ,
①当m何值时,y是x的正比例函数?
②当m何值时,y是x的反比例函数?(上述两个问均要求写出解析式)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com