
【题目】如图,已知菱形ABCD的边长为2,∠DAB=60°,E、F分别是AD、CD上的两个动点,且满足AE+CF=2.连接BD.
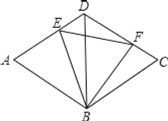
(1)图中有几对三角形全等?试选取一对全等的三角形给予证明;
(2)判断△BEF的形状,并说明理由.
(3)当△BEF的面积取得最小值时,试判断此时EF与BD的位置关系.
【答案】(1)△BAE≌△BDF,△BDE≌△BCF,△BAD≌△BCD,共三对;证明见解析;(2)△BEF为正三角形.理由见解析;(3)此时BD垂直平分EF.
【解析】
(1)可根据题意判断出△BAD≌△BCD(SSS)
△BAE≌△BD(SAS)△BDE≌△BCF(SAS),任选一组证明即可.
(2)首先由(1)知△BDE≌△BCF,得到BE=BF,再根据∠DBE=∠CB,∠DBC=∠DBF+∠CBF=60,得到一个角为60°即可证明为等边三角形.
(3)设BE=BF=EF=x,由S△BEF=![]() ,即面积根x值有关,当x最小,即BE垂直于AD时面积最小.
,即面积根x值有关,当x最小,即BE垂直于AD时面积最小.
(1)△BAE≌△BDF,△BDE≌△BCF,△BAD≌△BCD,共三对;
证明:△BDE≌△BCF.
在△BDE和△BCF中,
 ,
,
故△BDE≌△BCF.
(2)△BEF为正三角形.
理由:∵△BDE≌△BCF,
∴∠DBE=∠CBF,BE=BF,
∵∠DBC=∠DBF+∠CBF=60°,
∴∠DBF+∠DBE=60°即∠EBF=60°,
∴△BEF为等边三角形;
(3)设BE=BF=EF=x,
则S△BEF=![]() xxsin60°=
xxsin60°=![]() x2,
x2,
当BE⊥AD时,x最小=2×sin60°=![]() ,此时△BEF的面积最小,
,此时△BEF的面积最小,
此时点E、F分别位于AD、CD的中点,
故此时BD垂直平分EF.


科目:初中数学 来源: 题型:
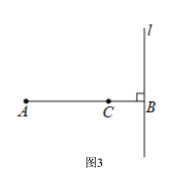
【题目】如图,直线l⊥线段AB于点B,点C在AB上,且AC=2CB,点M是直线l上的动点,作点B关于直线CM的对称点B’,直线AB’与直线CM相较于点P,联结PB.
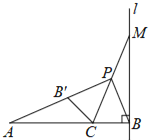
(1)如图1,若点P与点M重合,则∠PAB=_____°,线段PA与PB的比值为______.
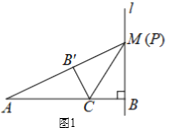
(2)如图2,若点P与点M不重合,设过P、B、C三点的圆与直线AP相交于点D,联结CD.
①求证:CD=CB’.
②求证:PA=2PB.
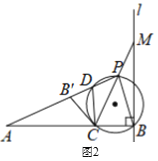
(3)如图③,AC=2,BC=1,则满足条件PA=2PB的点都在一个确定的圆上,在以下两小题中选做一题:
①如果你能发现这个确定圆的圆心和半径,那么不必写出发现过程,只要证明这个圆上的任意一点Q,都满足QA=2QB.
②如果你不能发现这个确定圆的圆心和半径,那么请取几个特殊位置的P点,如点P在直线AB上,点P与点M重合等进行探究,求这个圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝新中国成立70周年,河南省实验中学开展了以“我和我亲爱的祖国”为主题的“快闪”活动,九年级准备从两名男生和两名女生中选出两名同学领唱,如果每一位同学被选中的机会均等,则选出的恰为一位男生一位女生的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
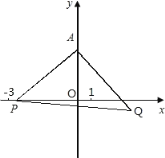
【题目】如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,将线段AP绕点A逆时针旋转90°,得到线段AQ,当点P从点(3,0)运动到点(1,0)时,点Q运动的路径长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
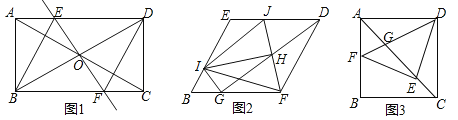
【题目】如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AC于点E,交BC于点F,连接BE、DF,且BE平分∠ABD.
(1)①求证:四边形BFDE是菱形;②求∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的数量关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
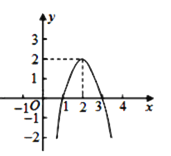
(1)写出方程ax2+bx+c=0的两个根;
(2)写出y随x的增大而减小的自变量x的取值范围;
(3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
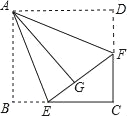
【题目】如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
(1)求证:四边形ABCD是正方形;
(2)求证:三角形ECF的周长是四边形ABCD周长的一半;
(3)若EC=FC=1,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
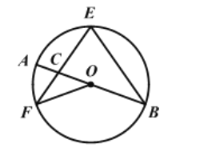
A.20°B.35°C.40°D.55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是边长为![]() 的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是
的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AH⊥EF;③AP2=PMPH;④EF的最小值是![]() .其中正确结论是( )
.其中正确结论是( )

A. ①③ B. ②③ C. ②③④ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com