
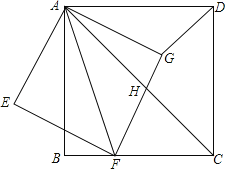
【题目】如图,正方形ABCD中,点F是BC边上一点,连结AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连结DG.
(1)填空:若∠BAF=18°,则∠DAG=______°.
(2)证明:△AFC∽△AGD;
(3)若![]() =
=![]() ,请求出
,请求出![]() 的值.
的值.
【答案】(1)27;(2)证明见解析;(3)![]() =
=![]() .
.
【解析】
(1)由四边形ABCD,AEFG是正方形,得到∠BAC=∠GAF=45°,于是得到∠BAF+∠FAC=∠FAC+∠GAC=45°,推出∠HAG=∠BAF=18°,由于∠DAG+∠GAH=∠DAC=45°,于是得到结论;
(2)由四边形ABCD,AEFG是正方形,推出![]() =
=![]() =
=![]() ,得
,得![]() =
=![]() ,由于∠DAG=∠CAF,得到△ADG∽△CAF,列比例式即可得到结果;
,由于∠DAG=∠CAF,得到△ADG∽△CAF,列比例式即可得到结果;
(3)设BF=k,CF=2k,则AB=BC=3k,根据勾股定理得到AF=![]() =
=![]() =
=![]() k,AC=
k,AC=![]() AB=3
AB=3![]() k,由于∠AFH=∠ACF,∠FAH=∠CAF,于是得到△AFH∽△ACF,得到比例式即可得到结论.
k,由于∠AFH=∠ACF,∠FAH=∠CAF,于是得到△AFH∽△ACF,得到比例式即可得到结论.
解:(1)∵四边形ABCD,AEFG是正方形,
∴∠BAC=∠GAF=45°,
∴∠BAF+∠FAC=∠FAC+∠GAC=45°,
∴∠HAG=∠BAF=18°,
∵∠DAG+∠GAH=∠DAC=45°,
∴∠DAG=45°﹣18°=27°,
故答案为:27.
(2)∵四边形ABCD,AEFG是正方形,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠DAG+∠GAC=∠FAC+∠GAC=45°,
∴∠DAG=∠CAF,
∴△AFC∽△AGD;
(3)∵![]() =
=![]() ,
,
设BF=k,
∴CF=2k,则AB=BC=3k,
∴AF=![]() =
=![]() =
=![]() k,AC=
k,AC=![]() AB=3
AB=3![]() k,
k,
∵四边形ABCD,AEFG是正方形,
∴∠AFH=∠ACF,∠FAH=∠CAF,
∴△AFH∽△ACF,
∴![]() ,
,
∴![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
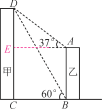
【题目】如图,某小区有甲、乙两座楼房,楼间距BC为50米,在乙楼顶部A点测得甲楼顶部D点的仰角为37°,在乙楼底部B点测得甲楼顶部D点的仰角为60°,则甲、乙两楼的高度分别为多少?(结果精确到1米,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
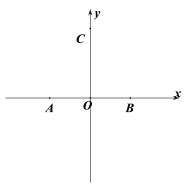
【题目】如图,在平面直角坐标系中,点A与点B关于原点O对称,点A![]() ,点C
,点C![]() ,点P在直线BC上运动.
,点P在直线BC上运动.
(1)连接AC、BC,求证:△ABC是等边三角形;
(2)求点P的坐标,使∠APO=![]() ;
;
(3)在平面内,平移直线BC,试探索:当BC在不同位置时,使∠APO=![]() 的点P的个数是否保持不变?若不变,指出点P的个数有几个?若改变,指出点P的个数情况,并简要说明理由.
的点P的个数是否保持不变?若不变,指出点P的个数有几个?若改变,指出点P的个数情况,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
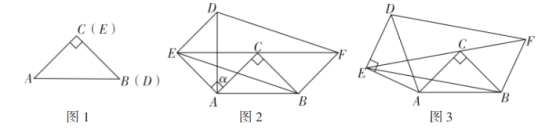
【题目】(1)如图1,E是正方形ABCD边AB上的一点,连接BD、DE,将∠BDE绕点D逆时针旋转90°,旋转后角的两边分别与射线BC交于点F和点G.
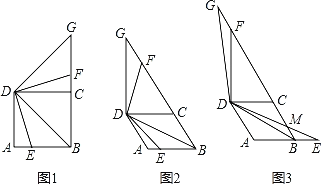
①线段DB和DG的数量关系是 ;
②写出线段BE,BF和DB之间的数量关系.
(2)当四边形ABCD为菱形,∠ADC=60°,点E是菱形ABCD边AB所在直线上的一点,连接BD、DE,将∠BDE绕点D逆时针旋转120°,旋转后角的两边分别与射线BC交于点F和点G.
①如图2,点E在线段AB上时,请探究线段BE、BF和BD之间的数量关系,写出结论并给出证明;
②如图3,点E在线段AB的延长线上时,DE交射线BC于点M,若BE=1,AB=2,直接写出线段GM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=﹣1.
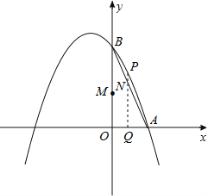
(1)求抛物线对应的函数关系式;
(2)动点Q从点O出发,以每秒1个单位长度的速度在线段OA上运动,同时动点M从M从O点出发以每秒3个单位长度的速度在线段OB上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒.
①当t为何值时,四边形OMPQ为矩形;
②△AON能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 和
和![]() 是两个完全重合在一起的等腰直角三角形,
是两个完全重合在一起的等腰直角三角形,![]() .现将
.现将![]() 固定,将
固定,将![]() 绕点
绕点![]() 按逆时针方向旋转,旋转角为
按逆时针方向旋转,旋转角为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)如图2,当![]() 时,判断四边形
时,判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)如图3,当![]() 时,(1)中的结论是否仍然成立?说明理由.
时,(1)中的结论是否仍然成立?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com