
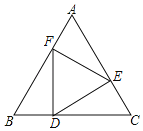
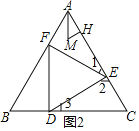
【题目】如图,边长为a的正△ABC内有一边长为b的内接正△DEF,则△AEF的内切圆半径为_____(用含a、b的代数式表示).
【答案】![]() (a﹣b).
(a﹣b).
【解析】
根据切线长定理得到AD=AE=![]() (AB+ACBC),证明△AEF≌△CDE≌△BFD,根据正切的概念计算.
(AB+ACBC),证明△AEF≌△CDE≌△BFD,根据正切的概念计算.
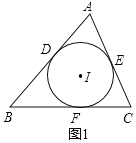
解:如图(1),⊙I是△ABC的内切圆,由切线长定理可得:AD=AE,BD=BF,CE=CF,
AD=AE=![]() [(AB+AC)﹣(BD+CE)]
[(AB+AC)﹣(BD+CE)]
=![]() [(AB+AC)﹣(BF+CF)]
[(AB+AC)﹣(BF+CF)]
=![]() (AB+AC﹣BC),
(AB+AC﹣BC),
在图(2)中,由于△ABC,△DEF都为正三角形,
∴AB=BC=CA,EF=FD=DE,∠BAC=∠B=∠C=∠FED=∠EFD=∠EDF=60°,
∴∠1+∠2=∠2+∠3=120°,∠1=∠3;
∴△AEF≌△CDE(AAS),
同理可证:△AEF≌△CDE≌△BFD,
∴BF=AE,即AF+AE=AF+BF=a.
设M是△AEF的内心,MH⊥AC于H,
则AH=![]() (AE+AF﹣EF)=
(AE+AF﹣EF)=![]() (a﹣b),
(a﹣b),
∵MA平分∠BAC,
∴∠HAM=30°;
∴HM=AHtan30°=![]() (a﹣b)
(a﹣b)![]() =
=![]() (a﹣b),
(a﹣b),
故答案为:![]() (a﹣b).
(a﹣b).


科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,点A、B的坐标分别为(9,0)、(6,﹣9),△AB'O'是△ABO关于点A的位似图形,且O'的坐标为(﹣3,0),则点B'的坐标为( )
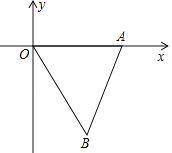
A.(8,﹣12)B.(﹣8,12)
C.(8,﹣12)或(﹣8,12)D.(5,﹣12)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为1的等腰直角△OA1A2,∠OA2A1=90°,且OA2为斜边在△OA1A2外作等腰直角△OA2A3,以OA3为斜边在△OA2A3外作等腰直角△OA3A4,以OA4为斜边在△OA3A4外作等腰直角△OA4A5,…连接A1A3,A3A5,A5A7,…分别与OA2,OA4,OA6,…交于点B1,B2,B3,…按此规律继续下去,记△OB1A3的面积为S1,△OB2A5的面积为S2,△OB3A7的面积为S3,…△OBnA2n+1的面积为Sn,则Sn=__(用含正整数n的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点F是BC边上一点,连结AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连结DG.
(1)填空:若∠BAF=18°,则∠DAG=______°.
(2)证明:△AFC∽△AGD;
(3)若![]() =
=![]() ,请求出
,请求出![]() 的值.
的值.
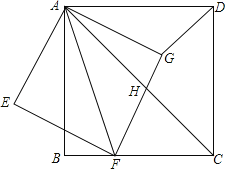
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若CD=4,⊙O的直径为10,求BD的长度.
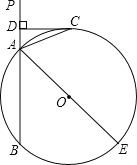
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,以点C为坐标原点,点![]() ,
,![]() ,将
,将![]() 绕点A顺时针旋转90°.
绕点A顺时针旋转90°.
(1)在图中画出旋转后的![]() ,并写出点
,并写出点![]() 、
、![]() 的坐标;
的坐标;
(2)已知点![]() ,在x轴上求作一点P(注:不要求写出P点的坐标),使得PD的值最小,并求出
,在x轴上求作一点P(注:不要求写出P点的坐标),使得PD的值最小,并求出![]() 的最小值;
的最小值;
(3)写出![]() 在旋转过程中,线段AB扫过的面积
在旋转过程中,线段AB扫过的面积
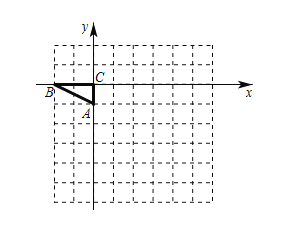
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设直线y=kx+6和直线y=(k+1)x+6(k是正整数)及x轴围成的三角形面积为Sk(k=1,2,3,…,8),则S1+S2+S3+…+S8的值是( )
A. ![]() B.
B. ![]() C. 16D. 14
C. 16D. 14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.

(1)求反比例函数和一次函数的解析式;
(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com