
����Ŀ����1����ͼ1��E��������ABCD��AB�ϵ�һ�㣬����BD��DE������BDE�Ƶ�D��ʱ����ת90�㣬��ת��ǵ����߷ֱ�������BC���ڵ�F�͵�G��
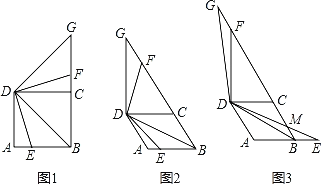
���߶�DB��DG��������ϵ���� ����
��д���߶�BE��BF��DB֮���������ϵ��
��2�����ı���ABCDΪ���Σ���ADC��60�㣬��E������ABCD��AB����ֱ���ϵ�һ�㣬����BD��DE������BDE�Ƶ�D��ʱ����ת120�㣬��ת��ǵ����߷ֱ�������BC���ڵ�F�͵�G��
����ͼ2����E���߶�AB��ʱ����̽���߶�BE��BF��BD֮���������ϵ��д�����۲�����֤����
����ͼ3����E���߶�AB���ӳ�����ʱ��DE������BC�ڵ�M����BE��1��AB��2��ֱ��д���߶�GM�ij��ȣ�
���𰸡���1����DB��DG����BF+BE��![]() BD����2����BF+BE��
BD����2����BF+BE��![]() BD�����ɼ���������GM��
BD�����ɼ���������GM��![]() .
.
��������
��1���ٸ�����ת�����ʽ�ɣ�
�ڸ��������ε����ʺ�ȫ�������ε��ж������ʽ�ɣ�
��2���ٸ������ε����ʺ�ȫ�������ε��ж������ʽ�ɣ�
���������ߣ�����BD��BF�ij�������ƽ���߷��߶γɱ��������ɵ�BM�ij��������߶εIJ�ɵý��ۣ�
�⣺��1����DB��DG��
�����ǣ�
�ߡ�DBE�Ƶ�B��ʱ����ת90�㣬��ͼ1��
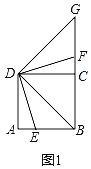
����ת��֪����BDE����FDG����BDG��90�㣬
���ı���ABCD�������Σ�
���CBD��45�㣬
���G��45�㣬
���G����CBD��45�㣬
��DB��DG��
�ʴ�Ϊ��DB��DG��
��BF+BE��![]() BD���������£�
BD���������£�
����֪����FDG����EDB����G����DBE��45�㣬BD��DG��
���FDG�ա�EDB��ASA����
��BE��FG��
��BF+FG��BF+BE��BC+CG��
Rt��DCG�У��ߡ�G����CDG��45�㣬
��CD��CG��CB��
��DG��BD��![]() BC��
BC��
��BF+BE��2BC��![]() BD��
BD��
��2������ͼ2��BF+BE��![]() BD��
BD��
�������£�������ABCD�У���ADB����CDB��![]()
![]() ��ADC��
��ADC��![]() ��60�㣽30�㣬
��60�㣽30�㣬
����ת120��á�EDF����BDG��120�㣬��EDB����FDG��
�ڡ�DBG�У���G��180�㩁120�㩁30�㣽30�㣬
���DBG����G��30�㣬
��DB��DG��
���EDB�ա�FDG��ASA����
��BE��FG��
��BF+BE��BF+FG��BG��
����D��DM��BG�ڵ�M����ͼ2��
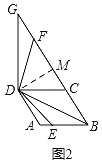
��BD��DG��
��BG��2BM��
��Rt��BMD�У���DBM��30�㣬
��BD��2DM��
��DM��a����BD��2a��
BM��![]() a��
a��
��BG��2![]() a��
a��
��![]() ��
��![]() ��
��
��BG��![]() BD��
BD��
��BF+BE��BG��![]() BD��
BD��
������A��AN��BD��N����D��DP��BG��P����ͼ3��
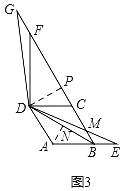
Rt��ABN�У���ABN��30�㣬AB��2��
��AN��1��BN��![]() ��
��
��BD��2BN��2![]() ��
��
��DC��BE��
��![]() ��
��![]() ��
��
��CM+BM��2��
��BM��![]() ��
��
Rt��BDP�У���DBP��30�㣬BD��2![]() ��
��
��BP��3��
����ת�ã�BD��BF��
��BF��2BP��6��
��GM��BG��BM��6+1��![]() ��
��![]()


 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Գ���Ϊֱ��![]() ��������
��������![]() ��x���ཻ��A��B���㣬����A�������Ϊ����3��0����
��x���ཻ��A��B���㣬����A�������Ϊ����3��0����

��1�����B�����ꣻ
��2����֪![]() ��CΪ��������y��Ľ��㡣
��CΪ��������y��Ľ��㡣
������P���������ϣ���![]() �����P�����ꣻ
�����P�����ꣻ
�����Q���߶�AC�ϵĶ��㣬��QD��x�ύ�������ڵ�D�����߶�QD���ȵ����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʱ��2019��3��10��0ʱ28�֣��ҹ����������Ƿ��������ó������������ػ�����ɹ�������![]() ���Ƿ������գ����ǽ���Ԥ�����.��ͼ�����Ǵӵ���
���Ƿ������գ����ǽ���Ԥ�����.��ͼ�����Ǵӵ���![]() �����䣬������ﵽ
�����䣬������ﵽ![]() ��ʱ����λ�ڵ����״�վ
��ʱ����λ�ڵ����״�վ![]() �����
�����![]() �ľ�����
�ľ�����![]() ������Ϊ
������Ϊ![]() ��1���������
��1���������![]() �㣬���
�㣬���![]() ������Ϊ
������Ϊ![]() .(�ο����ݣ�sin42.4���0.67��cos42.4���0.74��tan42.4���0.905��sin45.5���0.71��cos45.5����0.70��tan45.5���1.02)
.(�ο����ݣ�sin42.4���0.67��cos42.4���0.74��tan42.4���0.905��sin45.5���0.71��cos45.5����0.70��tan45.5���1.02)
(��)����̨���״�վ֮��ľ���![]() ��
��
(��)����ö�����![]() ��
��![]() ��ƽ���ٶ��Ƕ���(�����ȷ��0.01)��
��ƽ���ٶ��Ƕ���(�����ȷ��0.01)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����Ϊ1�ĵ���ֱ�ǡ�OA1A2����OA2A1=90�㣬��OA2Ϊб���ڡ�OA1A2��������ֱ�ǡ�OA2A3����OA3Ϊб���ڡ�OA2A3��������ֱ�ǡ�OA3A4����OA4Ϊб���ڡ�OA3A4��������ֱ�ǡ�OA4A5��������A1A3��A3A5��A5A7�����ֱ���OA2��OA4��OA6�������ڵ�B1��B2��B3�������˹��ɼ�����ȥ���ǡ�OB1A3�����ΪS1����OB2A5�����ΪS2����OB3A7�����ΪS3������OBnA2n+1�����ΪSn����Sn=__���ú�������n��ʽ�ӱ�ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
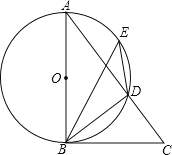
����Ŀ����ͼ��AB����O��ֱ������E��![]() �ϵ�һ�㣬��DBC=��BED��
�ϵ�һ�㣬��DBC=��BED��
��1����֤��BC����O�����ߣ�
��2����֪AD=3��CD=2����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
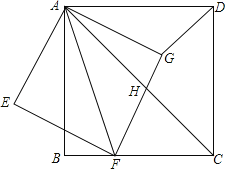
����Ŀ����ͼ��������ABCD�У���F��BC����һ�㣬����AF����AFΪ�Խ�����������AEFG����FG��������ABCD�ĶԽ���AC�ཻ�ڵ�H������DG.
(1)��գ�����BAF��18�������DAG��______��.
(2)֤������AFC�ס�AGD��
(3)��![]() ��
��![]() �������
�������![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
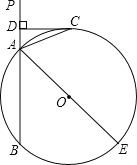
����Ŀ����ͼ����ֱ֪��PA����O��A��B���㣬AE�ǡ�O��ֱ������CΪ��O��һ�㣬��ACƽ�֡�PAE����C��CD��PA������ΪD��
��1����֤��CDΪ��O�����ߣ�
��2����CD��4����O��ֱ��Ϊ10����BD�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������з��̣�
��1��2x��x+1����2x+2
��2��x2��4x��4��0
��3��x2��![]() x��7��0
x��7��0
��4����x��1��2��5��x��1����6��0
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com