
����Ŀ��ij�߲˾�����ȥ�߲�������������ij���߲ˣ���֪�����߲˵���������20ǧ�ˡ�60ǧ��֮�䣨��20ǧ�˺�60ǧ�ˣ�ʱ��ÿǧ����������5Ԫ��������60ǧ��ʱ�������������߲�ȫ������ۣ�
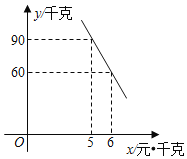
��1�������飬���߲˾��������۸����߲˵���������y��ǧ�ˣ������ۼ�x��Ԫ/ǧ�ˣ���һ�κ�����ϵ����ͼ����ͼ�����y��x֮��ĺ�����ϵʽ��
��2�������߲˾�����ÿ�����۴����߲˲�����75ǧ�ˣ��ҵ������ۼ۲��䣬��ô���ۼ۶�Ϊ����ʱ���þ��������۴����߲˵ĵ�����������������Ϊ����Ԫ��
���𰸡���1��y����30x+240����2�����ۼ۶�Ϊ5.5Ԫʱ�����տɻ����������������Ϊ112.5Ԫ
��������
��1�����ô���ϵ�������ѵ㣨5��90������6��60������һ�κ�������ʽ���������ϵ�����ɣ�
��2���赱�տɻ�����w��Ԫ���������ۼ�ΪxԪ�����ݵڣ�1���ʼ������г�����w��x�ĺ�����ϵʽ���ٸ��ݶ��κ�����ͼ������ʼ�ʵ�����壨��30x+240��75����x��5.5���ó����ֵ.
�⣺��1�����һ�κ�������ʽΪy��kx+b��k��0�����ѵ㣨5��90������6��60�����룬��
![]() ��
��
���![]() ��
��
�ʸ�һ�κ�������ʽΪ��y����30x+240��
��2���赱�տɻ�����w��Ԫ���������ۼ�ΪxԪ���ɣ�1��֪��
w������30x+240����x��5��0.8����-30x2+360x-960
=��30��x��6��2+120����30x+240��75����x��5.5��
��x��5.5ʱ�����տɻ����������������Ϊ112.5Ԫ��


 ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д� �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��12������������ʡ�人�в���ҽԺ½�����ֲ���ԭ����ײ���������֤ʵ�÷���Ϊһ������״������Ⱦ�ķ��ף��䴫Ⱦ�Խ�ǿ.Ϊ����Ч�ر��⽻���Ⱦ����Ҫ��ȡ���·�����ʩ���ٴ����֣�����ϴ�֣����ٳ��ţ����ظ��룻����ڱǣ������ԣ�ij��˾Ϊ�˽�Ա���Է�����ʩ���˽�̶ȣ��������˽⡢�˽���١������˽�ͺ��˽⣩��ͨ�������ʾ�����ķ�ʽ����������������飨ÿ��Ա��������ֻ��ѡ��һ����������������Ƴ���������ͳ��ͼ��
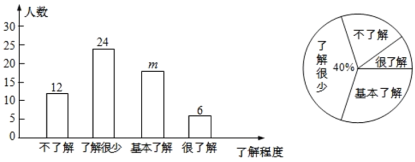
��������������Ϣ�������������
��1�����ι�������_______��Ա��������ͳ��ͼ��![]() ________��
________��
��2�����ù�˾����Ա��1000����������Ʋ��˽������ʩ��������
��3���ڵ����У�������4��Ա���Է�����ʩ���˽⣬������3����Ա����1��ŮԱ��.�����������������ȡ2���������ڹ�˾Ⱥ���ռ�������ʩ����ǡ�ó���һ��һŮ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ���ڡ�O�У�ֱ��AB����CD��G��EΪDC�ӳ�����һ�㣬BE����O�ڵ�F��
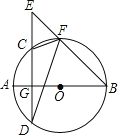
��1����֤����EFC����BFD��
��2����FΪ��Բ��AB���е㣬��2BF��3EF����tan��EFC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������鸴ѧ��ѧУ��չ�˶�����ʽ�ķ���֪ʶ��������������ȫԱ�μӵ���������֪ʶ�������Ծ���Ŀ��10�⣬ÿ��10�֣��ֱַ�����꼶1,2,3���и������ȡ10��ͬѧ�ijɼ�����λ���֣���
�ռ������������£�
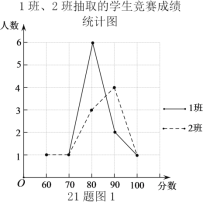
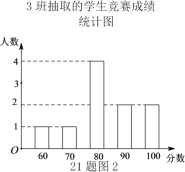
�������ݣ�
ƽ���� | ��λ�� | ���� | |
1�� | 83 |
| 80 |
2�� | 83 |
|
|
3�� |
| 80 | 80 |
����������Ϣ�ش��������⣺
��1����ֱ��д��������![]() ��
��![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
��2���Ƚ��������������ݵ�ƽ��������λ��������������Ϊ�ĸ���ijɼ��ȽϺã���˵�����ɣ�һ�����ɼ��ɣ���
��3��Ϊ����ѧ�����Ӱ�ȫ֪ʶ��ѧϰ��ѧУ���������ɼ����ֵ�ͬѧ�䷢��״����У���꼶ѧ����120�ˣ��Թ�����Ҫ�������Ž�״��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��C����һ���߿�̽�����ӵ�C�����ˮƽ������A��B����ĸ��Ƿֱ�Ϊ30����45������AB=2km����A��C����֮��ľ���Ϊ_____km��
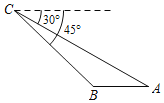
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �ı߳�Ϊ4����
�ı߳�Ϊ4����![]() �ڶԽ���
�ڶԽ���![]() �ϣ������
�ϣ������![]() �غϣ���
�غϣ���![]() ����
����![]() �������εı��ϣ������ĸ������У�
�������εı��ϣ������ĸ������У�
�ٴ����������ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
�ڴ����������ı���![]() �����Σ�
������
�۴����������ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
�����ٴ���һ���ı���![]() �������Σ�
��������
������ȷ���۵������_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����۾���ֽƬABCD��ʹAD��BC�غϣ��õ��ۺ�EF����ֽƬչƽ���ٴ��۵�ֽƬ��ʹ��A����EF�ϵĵ�N������ʹ�ۺ۾�����B���õ��ۺ�BM����չƽֽƬ������MN��BN�����н���һ����ȷ���ǣ� ��
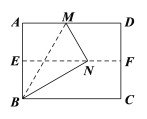
A.![]() B.
B.![]()
C.BM��EN����ƽ��D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
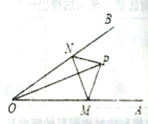
����Ŀ����ͼ����![]() ��
��![]() ������㣬
������㣬![]() �ֱ�������OA��������OB�ϵĶ��㣬
�ֱ�������OA��������OB�ϵĶ��㣬![]() �ܳ�����СֵΪ8cm����
�ܳ�����СֵΪ8cm����![]() �Ķ����ǣ� ��
�Ķ����ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С����Ƶ�������֪�����ε�һ����ȡһ�㣬ʹ����㵽��������ε��������ߵľ���������ij߹���ͼ���̣�
��֪����ABC��
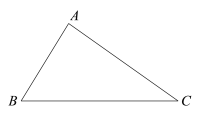
��������D��ʹ�õ�D��BC���ϣ��ҵ�AB��AC�ߵľ�����ȣ�
��������ͼ��
����BAC��ƽ���ߣ���BC�ڵ�D�����D��Ϊ����
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�� (������ͼ�ۼ�)��
��2����������֤����
֤������DE��AB�ڵ�E����DF��AC�ڵ�F��
��ADƽ�֡�BAC��
�� = ( ) (������������) ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com