Question

18．如图，已知正方形ABCD的边长为10，以AB边为直径向外作半圆O，点E是半圆O上与点A、B不重合的任意一点，过点E作CB所在直线的垂线，垂足为点F．
（1）证明：△ABE∽△BEF；
（2）当△BCE=30°时，CE与AB交于点P，求$\frac{AP}{PB}$的值；
（3）当CE经过圆心O的时候，求tan∠EAB的值．

Answer 1

分析 （1）根据圆周角定理得到∠AEB=90°，得到∠AEB=∠EFB，根据平行线的性质得到∠FEB=∠EBA，根据相似三角形的判定定理证明即可；
（2）根据题意和正切的定义求出PB的长，根据正方形的性质求出AP的长，计算即可；
（3）作EG⊥AB于G，根据勾股定理求出PC的长，证明△EGP∽△CBP，根据相似三角形的性质求出EG，根据勾股定理求出GP，根据正切的定义计算即可．

解答 （1）证明：∵四边形ABCD是正方形，
∴∠ABC=90°，又EF⊥BC，
∴EF∥AB，
∴∠FEB=∠EBA，
∵AB为半圆O的直径，
∴∠AEB=90°，
∴∠AEB=∠EFB，又∠FEB=∠EBA，
∴△ABE∽△BEF；
（2）∵∠BCE=30°，BC=10，
∴PB=BC•tan∠BCE=$\frac{10\sqrt{3}}{3}$，
∴AP=10-$\frac{10\sqrt{3}}{3}$，
∴$\frac{AP}{PB}$=$\frac{10-\frac{10\sqrt{3}}{3}}{\frac{10\sqrt{3}}{3}}$=$\sqrt{3}$-1；
（3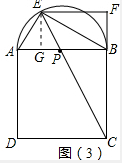）如图（3），作EG⊥AB于G，
∵CE经过圆心O，
∴PA=PE=PB=5，
∴CP=$\sqrt{P{B}^{2}+B{C}^{2}}$=5$\sqrt{5}$，
∵EG∥BC，
∴△EGP∽△CBP，
∴$\frac{EG}{BC}$=$\frac{EP}{PC}$，即$\frac{EG}{10}$=$\frac{5}{5\sqrt{5}}$，
解得，EG=2$\sqrt{5}$，
∴GP=$\sqrt{E{P}^{2}-E{G}^{2}}$=$\sqrt{5}$，
∴AG=5-$\sqrt{5}$，
∴tan∠EAB=$\frac{EG}{AG}$=$\frac{2\sqrt{5}}{5-\sqrt{5}}$=$\frac{\sqrt{5}+1}{2}$．

点评 本题考查的是相似三角形知识的综合运用，掌握相似三角形的判定定理和性质定理、正方形的性质、圆周角定理是解题的关键，解答时，注意正确作出辅助线、灵活运用数形结合思想．