
【题目】在△ABC中,CO是AB边上的中线,∠AOC=60°,AB=2,点P是直线OC上的一个动点,则当△PAB为直角三角形时,边AP的长为_____.
【答案】![]() 或
或![]() 或1
或1
【解析】
当∠ABP=90°时,如图2,易得∠BOP=60°,进而可利用三角函数求出BP的长,再根据勾股定理即可求出AP的长;当∠APB=90°时,分两种情况讨论:①如图1,点P在CO的延长线上时,利用直角三角形的性质可得PO=BO,进而可得△BOP为等边三角形,然后利用锐角三角函数可得AP的长;②如图3,点P在CO上时,易证△AOP为等边三角形,再利用等边三角形的性质可得结论.
解:如图1,当∠APB=90°,点P在CO的延长线上时,
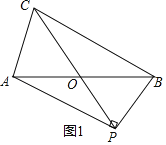
∵AO=BO,∴PO=BO,
∵∠AOC=60°,∴∠BOP=60°,
∴△BOP为等边三角形,
∴∠ABP=60°,
∵AB=2,
∴AP=ABsin60°=2×![]() ;
;
如图2,当∠ABP=90°时,
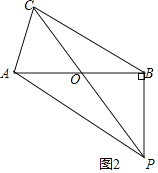
∵∠AOC=∠BOP=60°,
∴BP=![]() ,
,
在直角△ABP中,由勾股定理,得AP=![]() ;
;
如图3,当∠APB=90°时,点P在CO上时,
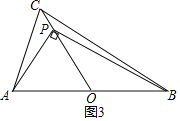
∵AO=BO,∠APB=90°,
∴PO=AO,
∵∠AOC=60°,
∴△AOP为等边三角形,
∴AP=AO=1;
综上,AP=![]() 或
或![]() 或1.
或1.
故答案为:![]() 或
或![]() 或1.
或1.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】 在平面直角坐标系中,有两条抛物线关于x轴对称,且它们的顶点相距6个单位长度,若其中一条抛物线的函数表达式为y=﹣x2+4x+2m,则m的值是( )
A.![]() B.
B.![]() C.1D.
C.1D.![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD,CD,过点D作PD∥BC与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:BD2=PBAC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学活动小组在一次活动中,对一个数学问题做了如下研究:
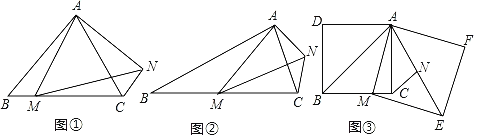
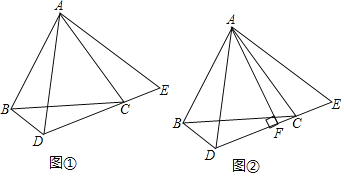
(问题发现)(1)如图①,在等边三角形ABC中,点M是BC边上任意一点,连接AM,以AM为边作等边三角形AMN,连接CN,则∠ABC和∠ACN的数量关系为 ;
(变式探究)(2)如图②,在等腰三角形ABC中,AB=BC,点M是BC边上任意一点(不含端点B,C,连接AM,以AM为边作等腰三角形AMN,使∠AMN=∠ABC,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;
(解决问题)(3)如图③,在正方形ADBC中,点M为BC边上一点,以AM为边作正方形AMEF,点N为正方形AMEF的中心,连接CN,AB,AE,若正方形ADBC的边长为8,CN=![]() ,直接写出正方形AMEF的边长.
,直接写出正方形AMEF的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.
(1)若购买这两类球的总金额为4600元,求篮球、足球各买了多少个?
(2)若购买篮球的总金额不超过购买足球的总金额,求最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,点D为平面内一点,连接DB、DC,∠BDC=120°.
(1)如图①,当点D在BC下方时,连接AD,延长DC到点E,使CE=BD,连接AE.
①求证:△ABD≌△ACE;
②如图②,过点A作AF⊥DE于点F,直接写出线段AF、BD、DC间的数量关系;
(2)若AB=2![]() ,DC=6,直接写出点A到直线BD的距离.
,DC=6,直接写出点A到直线BD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列分式方程解应用题:
“5G改变世界,5G创造未来”.2019年9月,全球首个5G上海虹桥火车站,完成了5G网络深度覆盖,旅客可享受到高速便捷的5G网络服务.虹桥火车站中5G网络峰值速率为4G网络峰值速率的10倍.在峰值速率下传输7千兆数据,5G网络比4G网络快630秒,求5G网络的峰值速率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠疫情初期,医用口罩是紧缺物资.某市为降低因购买口罩造成人群聚集的感染风险,通过APP实名预约,以摇号抽签的方式,由市民到指定门店购买口罩.规定:已中签者在本轮摇号结束前不再参与摇号;若指定门店当日市民购买口罩的平均等待时间超过8分钟,则次日必须增派工作人员.
(1)据APP数据统计:第一天有386.5万人进行网上预约,此后每天预约新增4万人,且每天有35.5万人中签,若小明第一天没有中签,则他第二天中签的概率是多少?
(2)该市某区指定A,B两门店每天8:00-22:00时段让中签市民排队购买口罩.图1是A门店某日购买口罩的人数与等待时间的统计图,为了算出A门店某日等待9分钟的人数,小红选择14:00~16:00这个时间段到店进行统计,统计结果见表1,且这个时间段的人数占该店当天等待9分钟人数的![]() .表2是B门店某日购买口罩的人数与等待时间的统计表.请你运用所学的统计知识判断A,B门店次日是否需要增派工作人员.
.表2是B门店某日购买口罩的人数与等待时间的统计表.请你运用所学的统计知识判断A,B门店次日是否需要增派工作人员.
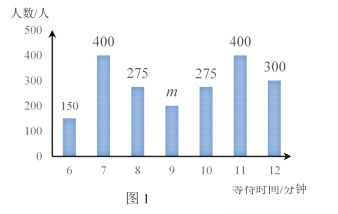
表1
时间段 | 等待9分钟/人 |
14:00~14:30 | 10 |
14:30~15:00 | 20 |
15:00~15:30 | 15 |
15:30~16:00 | 5 |
表2
等待时间 |
|
|
|
|
人数/人 |
|
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了防范疫情,顺利复学,某市教育局决定从甲、乙两地用汽车向![]() 两校运送口罩,甲、乙两地分别可提供口罩40万个,10万个,
两校运送口罩,甲、乙两地分别可提供口罩40万个,10万个,![]() 两校分别需要口罩30万个,20万个,两地到
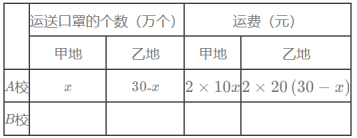
两校分别需要口罩30万个,20万个,两地到![]() 两校的路程如表(每万个口罩每千米运费2元),设甲地运往A校x万个口罩.
两校的路程如表(每万个口罩每千米运费2元),设甲地运往A校x万个口罩.
路程 | 路程 | |
甲地 | 乙地 | |
A校 | 10 | 20 |
B校 | 15 | 15 |
(1)根据题意,在答题卡中填写下表:
(2)设总运费为![]() 元,求
元,求![]() 与
与![]() 的函数关系式,当甲地运往A校多少万个口罩时,总运费最少?最少的运费是多少元?
的函数关系式,当甲地运往A校多少万个口罩时,总运费最少?最少的运费是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com