
����Ŀ��Ϊ�˷������飬˳����ѧ��ij�н����־����Ӽס���������������![]() ��У���Ϳ��֣��ס������طֱ���ṩ����40�����10�����
��У���Ϳ��֣��ס������طֱ���ṩ����40�����10�����![]() ��У�ֱ���Ҫ����30�����20��������ص�
��У�ֱ���Ҫ����30�����20��������ص�![]() ��У��·�������ÿ�������ÿǧ���˷�2Ԫ�����������AУx������֣�
��У��·�������ÿ�������ÿǧ���˷�2Ԫ�����������AУx������֣�
·�� | ·�� | |
�� | �ҵ� | |
AУ | 10 | 20 |
BУ | 15 | 15 |
��1���������⣬�ڴ������д�±���
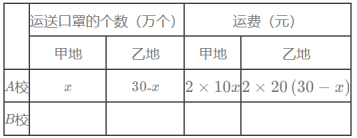
��2�������˷�Ϊ![]() Ԫ����
Ԫ����![]() ��
��![]() �ĺ�����ϵʽ����������AУ�����������ʱ�����˷����٣����ٵ��˷��Ƕ���Ԫ��
�ĺ�����ϵʽ����������AУ�����������ʱ�����˷����٣����ٵ��˷��Ƕ���Ԫ��
���𰸡���1������������2��������AУ30�������ʱ���˷����٣����ٵ��˷���1200Ԫ��
��������
��1���������⣬�ؿ��ṩ����40������Ѿ�����AУx�����������BУ40-x�����AУ��Ҫ����30���������Ҫ�ҵ�����30-x������ҵػ�ʣx-20�����������BУ��
�˷��ٸ��ݵ�һ������·�̺�ÿ�������ÿǧ���˷�2Ԫ���м��㼴�ɣ�
��2���Ѹ��Ե��˷���ӵõ�һ�κ�������![]() ��
��![]() ��֪����
��֪����![]() ʱ��W��С,���������С�˷Ѽ��ɣ�
ʱ��W��С,���������С�˷Ѽ��ɣ�
�⣺��1��
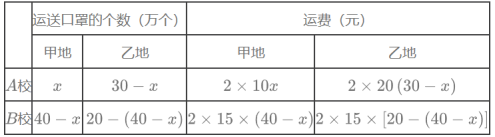
��2��![]()
![]()
��![]() ������W��x���������
������W��x���������
���Ե�![]() ʱ��W��С����Сֵ��
ʱ��W��С����Сֵ��![]()
�������AУ30�������ʱ���˷����٣����ٵ��˷���1200Ԫ��


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�CO��AB���ϵ����ߣ���AOC��60�㣬AB��2����P��ֱ��OC�ϵ�һ�����㣬��PABΪֱ��������ʱ����AP�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
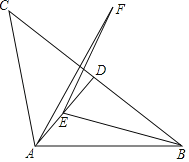
����Ŀ�� ��ͼ����ABC�У�AB��AC����ABC������tan����![]() ��AD��BC�ڵ�D����E���߶�AD�ϵ�һ�����㣬����EB�����߶�EB�Ƶ�E��ʱ����ת2����õ��߶�EF������AF����BC��24�����߶�AF����СֵΪ_____��
��AD��BC�ڵ�D����E���߶�AD�ϵ�һ�����㣬����EB�����߶�EB�Ƶ�E��ʱ����ת2����õ��߶�EF������AF����BC��24�����߶�AF����СֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=2��AD=3��E��F�ֱ���AD��CD�ϵĶ��㣬EF=2��Q��EF���е㣬PΪBC�ϵĶ��㣬����AP��PQ����AP+PQ����Сֵ����(����)
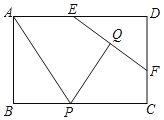
A.2B.3C.4D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���ں���y�����dzƺ�����������|y|����ֵ���������磺����y![]() ����ֵ����Ϊy=|
����ֵ����Ϊy=|![]() |��
|��
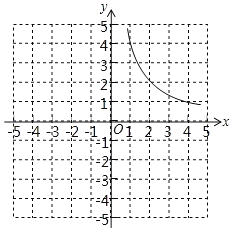
��ͼ������y![]() (x��0)������ͼ�л���y=x+3����ֵ������ͼ��
(x��0)������ͼ�л���y=x+3����ֵ������ͼ��
��1��д��y=x+3����ֵ�������������ʣ�
��2��y=x+3����ֵ������ͼ����x�ᡢy�ᡢ����y![]() (x��0)�Ľ���ֱ���A��B��C����D���߶�AC��һ����(�������˵�)������D��x���ƽ���ߣ�����ֵ����ͼ������һ��E�������߽��ڵ�P��
(x��0)�Ľ���ֱ���A��B��C����D���߶�AC��һ����(�������˵�)������D��x���ƽ���ߣ�����ֵ����ͼ������һ��E�������߽��ڵ�P��
�������PAD����������ֵ��
��̽�����ڵ�D�˶��Ĺ����У��ı���PAEC�ܷ�Ϊƽ���ı��Σ����ܣ������ʱ��D�����ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м��㣺��![]() ���ڣ�x��2y��2��x2��4y2���ۣ���a��4a3����a7����x10��x5��x2�����д���ĸ����ǣ�������
���ڣ�x��2y��2��x2��4y2���ۣ���a��4a3����a7����x10��x5��x2�����д���ĸ����ǣ�������
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ȤС��Ժ���y��![]() ��ͼ������ʽ���̽���������������������⣺
��ͼ������ʽ���̽���������������������⣺
��1������y��![]() ���Ա���x��ȡֵ��Χ���� ��
���Ա���x��ȡֵ��Χ���� ��
��2�������x��y�ļ����Ӧֵ����m���� ��
x | �� | ��2 | ��1 | 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | �� |
y | �� |
| m |
| 0 | ��1 | 3 | 2 |
|
|
| �� |
��3����ͼ���Ѿ������˸ú���ͼ���һ���֣����㻭������ͼ�����һ���֣�
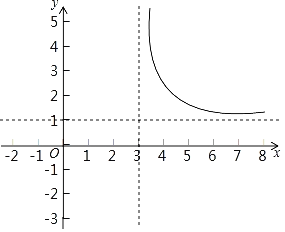
��4���ú���ͼ��������֧����һ��������ĶԳƣ��������������� ��
��5��������y��![]() ��ͼ����������A��x1��y1����B��x2��y2����C��x3��y3����x1��x2��3��x3����y1��y2��y3�Ĵ�С��ϵ���� �������������ӣ���
��ͼ����������A��x1��y1����B��x2��y2����C��x3��y3����x1��x2��3��x3����y1��y2��y3�Ĵ�С��ϵ���� �������������ӣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
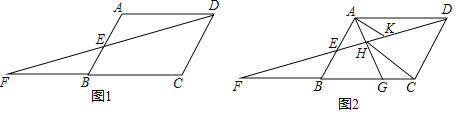
����Ŀ����֪����ͼ1����ABCD�У���E��AB�е㣬����DE���ӳ�����CB���ӳ����ڵ�F��
��1����֤����ADE�ա�BFE��
��2����ͼ2����G�DZ�BC������һ�㣨��G�����B��C�غϣ�������AG��DF�ڵ�H������HC������A��AK��HC����DF�ڵ�K��
����֤��HC=2AK��
�ڵ���G�DZ�BC�е�ʱ��ǡ��HD=nHK��nΪ������������n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
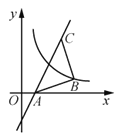
����Ŀ����ͼ������C(3,4)��ֱ��![]() ��
��![]() ���ڵ�A����ABC=90�㣬AB=CB������
���ڵ�A����ABC=90�㣬AB=CB������![]() ����B������A��
����B������A��![]() ��������ƽ��
��������ƽ��![]() ����λ����ǡ�����ڸ������ϣ���
����λ����ǡ�����ڸ������ϣ���![]() ��ֵΪ________��
��ֵΪ________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com