
 �������ϵĵ�P�������²������Ȱѵ�P��ʾ������2���ٰ��������Ķ�Ӧ������ƽ��1����λ���õ���P�Ķ�Ӧ��P�䣬�ֶ������ϵ�A��B�����������������õ����Ӧ��A�䡢B�䣮
�������ϵĵ�P�������²������Ȱѵ�P��ʾ������2���ٰ��������Ķ�Ӧ������ƽ��1����λ���õ���P�Ķ�Ӧ��P�䣬�ֶ������ϵ�A��B�����������������õ����Ӧ��A�䡢B�䣮���� ��1��������Ŀ�涨���Լ������ϵ�������ƽ���üӷ����㼴�������A�䣻
��2�����B��ʾ����Ϊa�����������г�������⼴�ɵõ���B��ʾ������
��3������t����M����A��B�ľ�����ȣ����������г����̼��㼴�ɵý⣮
��� �⣺��1������A��ʾ������-4�����A���ʾ������-4��2+1=-7���ʴ�Ϊ��-7��
��2�����B��ʾ����Ϊb��
��2b+1=41��
��ã�b=20��
�����ϱ�ʾ��ͼ�� ��
��
��3������t����M����A��B�ľ�����ȣ�
AM=4t-��-4+2t��=2t+4��BM=20-2t-4t=20-6t��
��2t+4=20-6t��
��ã�t=2��
2��4=8�����M��Ӧ������8��
����A���B�غ�ʱ��20-2t=2t-4����ã�t=6��
6��4=24�����M��Ӧ������24��
�ڴ��ڣ���M��ʾ����Ϊ$\frac{56}{9}$��$\frac{104}{3}$��
���� ���⿼����һԪһ�η��̵�Ӧ�ã�������Ŀ��Ϣ�����Ȿ�������ϵ�IJ���������Ȼ���г������ǽ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
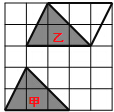 ��ͼ��ʾ����ͼ����Ӱ�������ɼ״�ƽ�����Ҵ�������ƽ�Ʒ�������ȷ���ǣ�������
��ͼ��ʾ����ͼ����Ӱ�������ɼ״�ƽ�����Ҵ�������ƽ�Ʒ�������ȷ���ǣ�������| A�� | �������ƶ�1���������ƶ�1�� | B�� | �������ƶ�3���������ƶ�1�� | ||
| C�� | �������ƶ�1���������ƶ�3�� | D�� | �������ƶ�3���������ƶ�3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -4 | B�� | 2 | C�� | -1 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com