解答:解:(1)①∵△ADC由△BOC旋转而成,
∴△ADC≌△BOC,
∴∠BCO=∠ACD,OC=CD,∠ADC=∠BOC=120°,
∵△ACB是等边三角形,
∴△OCD是等边三角形,
∴∠CDO=∠DOC=60°.
∴∠ADO=ADC-∠CDO=120°-60°=60°,
∵β=110°,α=120°,∠DOC=60°,
∴∠AOD=360°-110°-120°-60°=70°,
∴∠OAD=180°-70°-60°=50°.
故答案为:50°;
②∵△ADC由△BOC旋转而成,
∴△ADC≌△BOC,
∴∠BCO=∠ACD,OC=CD,∠ADC=∠BOC=100°,
∵△ACB是等边三角形,
∴△OCD是等边三角形,
∴∠CDO=∠DOC=60°.
∴∠ADO=ADC-∠CDO=100°-60°=40°,
∵β=120°,α=100°,∠DOC=60°,
∴∠AOD=360°-120°-100°-60°=80°,
∴∠OAD=180°-80°-40°=60°.
故答案为:60°;
③∵△ADC由△BOC旋转而成,
∴△ADC≌△BOC,
∴∠BCO=∠ACD,OC=CD,∠ADC=∠BOC=n°,
∵△ACB是等边三角形,
∴△OCD是等边三角形,
∴∠CDO=∠DOC=60°.
∴∠ADO=ADC-∠CDO=n°-60°,
∵β=130°,α=n°,∠DOC=60°,
∴∠AOD=360°-130°-n°-60°=170°-n°,
∴∠OAD=180°-∠AOD-∠ADO=180°-(170°-n°)-(n°-60°)=70°.
故答案为:70°;
④由①②③可知,④∠OAD与β有关,且∠OAD=β-60°.
(2)若△AOD是等腰三角形,
所以分三种情况:①∠AOD=∠ADO;②∠ODA=∠OAD;③∠AOD=∠DAO,
∵∠AOB=100°,∠COD=60°,
∴∠BOC=360°-100°-60°-∠AOD=200°-∠AOD,
而∠BOC=∠ADC=∠ADO+∠CDO,
由①∠AOD=∠ADO可得∠BOC=∠AOD+60°,
求得α=130°;
由②∠ODA=∠OAD可得α-60°+α-60°+200°-α=180°,
求得α=100°;
由③∠AOD=∠DAO可得200°-α+200°-α+α-60°=180°,
∠BOC=240°-2∠AOD,
求得α=160°;
综上可知α=130°、α=100°或α=160°.
①∵△OAD是等边三角形,
∴∠AOD=∠ADO=60°,
∵∠CDO=60°,△ADC由△BOC旋转而成,
∴α=∠ADO+∠CDO=120°.
∵∠AOD=∠DOC=60°,
∴β=360°-α-∠AOD-∠DOC=360°-120°-60°-60°=120°;
②能.
理由:若四边形ADCO能成为平行四边形,
∵∠OCD=60°,
∴∠OCD=∠ADO=60°,
∴∠AOC=∠ADC=
=
=120°,
∴当α=β=120°时,四边形ADCO是平行四边形.

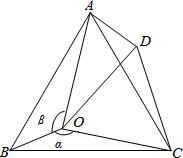 如图所示,点O是等边△ABC内一点,∠BOC=α,∠AOB=β(α、β均不是锐角),将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
如图所示,点O是等边△ABC内一点,∠BOC=α,∠AOB=β(α、β均不是锐角),将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.

 已知在纸面上有一数轴(如图),折叠纸面.
已知在纸面上有一数轴(如图),折叠纸面.