
【题目】根据下列条件,能画出唯一△ABC的有_____(填序号)
①![]() ,
,![]() ,
,![]() ;②AB=1,BC=2,AC=3;③AB=3,BC=4,
;②AB=1,BC=2,AC=3;③AB=3,BC=4,![]() ;④AB=3,BC=4,
;④AB=3,BC=4,![]() ;⑤AB=3,BC=4,
;⑤AB=3,BC=4,![]()
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】抛物线![]() 过点
过点![]() 和
和![]() ,点P为x轴正半轴上的一个动点,连接AP,在AP右侧作
,点P为x轴正半轴上的一个动点,连接AP,在AP右侧作![]() ,且
,且![]() ,点B经过矩形AOED的边DE所在的直线,设点P横坐标为t.
,点B经过矩形AOED的边DE所在的直线,设点P横坐标为t.
![]() 求抛物线解析式;
求抛物线解析式;
![]() 当点D落在抛物线上时,求点P的坐标;
当点D落在抛物线上时,求点P的坐标;
![]() 若以A、B、D为顶点的三角形与
若以A、B、D为顶点的三角形与![]() 相似,请直接写出此时t的值.
相似,请直接写出此时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将图1两个边长为1的正方形分割拼接成右边面积为2的正方形.
(1)请你直接写出图1中右边正方形的边长.
(2)请你同样用分割拼接的方法将图2中的五个边长为1正方形分割重新拼接成一个面积为5的正方形,画出切割拼接示意图,并如图1作出标记.(不必写出作法)
(3)设M=1+![]() ,
,![]() 是M的整数部分,b是M的小数部分,
是M的整数部分,b是M的小数部分,![]() 是
是![]() 的小数部分,求
的小数部分,求![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备用图甲所示的A型正方形板材和B型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
![]() 若该工厂准备用不超过10000元的资金去购买A,B两种型号板材,并全部制作竖式箱子,已知A型板材每张30元,B型板材每张90元,求最多可以制作竖式箱子多少只?
若该工厂准备用不超过10000元的资金去购买A,B两种型号板材,并全部制作竖式箱子,已知A型板材每张30元,B型板材每张90元,求最多可以制作竖式箱子多少只?
![]() 若该工厂仓库里现有A型板材65张、B型板材110张,用这批板材制作两种类型的箱子,问制作竖式和横式两种箱子各多少只,恰好将库存的板材用完?
若该工厂仓库里现有A型板材65张、B型板材110张,用这批板材制作两种类型的箱子,问制作竖式和横式两种箱子各多少只,恰好将库存的板材用完?
![]() 若该工厂新购得65张规格为
若该工厂新购得65张规格为![]() 的C型正方形板材,将其全部切割成A型或B型板材
的C型正方形板材,将其全部切割成A型或B型板材![]() 不计损耗
不计损耗![]() ,用切割成的板材制作两种类型的箱子,要求竖式箱子不少于20只,且材料恰好用完,则能制作两种箱子共______只
,用切割成的板材制作两种类型的箱子,要求竖式箱子不少于20只,且材料恰好用完,则能制作两种箱子共______只![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司准备把240吨白砂糖运往![]() 、
、![]() 两地,用大、小两种货车共20辆,恰好能一次性装完这批白砂糖,相关数据见下表:
两地,用大、小两种货车共20辆,恰好能一次性装完这批白砂糖,相关数据见下表:
载重量 | 运往 | 运往 | |
大车 | 15吨/辆 | 650元/辆 | 700元/辆 |
小车 | 10吨/辆 | 400元/辆 | 500元/辆 |
(1)求大、小两种货车各用多少辆?
(2)如果安排10辆货车前往![]() 地,其中大车有
地,其中大车有![]() 辆,其余货车前往
辆,其余货车前往![]() 地,且运往
地,且运往![]() 地的白砂糖不少于130吨.
地的白砂糖不少于130吨.
①![]() 的取值范围;
的取值范围;
②请设计出总运费最少的货车调配方案,并求最少总运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角三角形ABC中,![]() ,D为BC的中点,DE
,D为BC的中点,DE![]() AB,垂足为E,过点B作BF//AC交DE的延长线于点F.
AB,垂足为E,过点B作BF//AC交DE的延长线于点F.

(1)求证:![]() ;
;
(2)连接AF,求证:AF=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB和CD相交于点O,∠C=∠1,∠D=∠2,求证:∠A=∠B.

证明:∵∠C=∠1,∠D=∠2(已知)
又∵∠1=∠2( )
∴______(等量代换)
∴AC∥BD( )
∴____(两直线平行,内错角相等)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月![]() 按30天计算
按30天计算![]() ,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天
,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天![]() 且x为整数
且x为整数![]() 的销售量为y件.
的销售量为y件.
![]() 直接写出y与x的函数关系式;
直接写出y与x的函数关系式;
![]() 设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
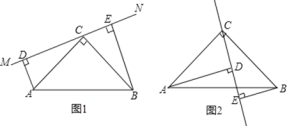
(1)求证:①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE又怎样的关系?并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com