Question

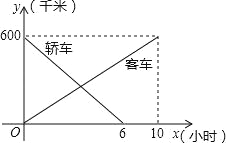
【题目】一辆客车从甲地开往乙地，一辆轿车从乙地开往甲地，两车同时出发，两车行驶x小时后，记客车离甲地的距离y1千米，轿车离甲地的距离y2千米，y1、y2关于x的函数图象如图所示：

①根据图象直接写出y1、y2关于x的函数关系式；

②当两车相遇时，求此时客车行驶的时间．

③相遇后，两车相距200千米时，求客车又行驶的时间．

Answer 1

【答案】①y1＝60x(0≤x≤10)，y2＝﹣100x+600(0≤x≤6)；②小时；③小时．

【解析】

（1）根据图象，用待定系数法求函数解析式；（2）结合（1），当两车相遇时，y1＝y2，即60x＝﹣100x+600；（3）结合图象，可得：相遇后相距200千米，则y1﹣y2＝200，即60x+100x﹣600＝200.

解：①设y1＝kx，则将(10，600)代入得出：600＝10k，

解得：k＝60，

∴y1＝60x (0≤x≤10)，

设y2＝ax+b，则将(0，600)，(6，0)代入得出：

，

解得：，

∴y2＝﹣100x+600 (0≤x≤6)；

②当两车相遇时，y1＝y2，即60x＝﹣100x+600

解得：x＝；

∴当两车相遇时，此时客车行驶了小时；

③相遇后相距200千米，则y1﹣y2＝200，即60x+100x﹣600＝200，

解得：x＝5

5﹣，

∴相遇后，两车相距200千米时，客车又行驶的时间小时．