
【题目】已知:![]() 分别是
分别是![]() 内角和外角平分线.
内角和外角平分线.

![]() 则
则![]() 的度数=_ ;
的度数=_ ;
![]() 求证:
求证:![]() ;
;
![]() 作
作![]() ,交
,交![]() 延长线于
延长线于![]() 的延长线交
的延长线交![]() 于
于![]() ,求证:
,求证:![]() .
.
【答案】(1)90°;(2)见解析;(3)见解析
【解析】
(1)根据角平分线的定义和邻补角的定义即可解得;
(2)过点C作CN∥AB交AE于点N,如图,易证CA=CN.由CN∥AB可得△ECN∽△EBA,则有![]() ,由CA=CN可得
,由CA=CN可得![]() ;
;
(3)分别延长BF、AC交于点H,证明△ABF≌△AHF,可得BF=HF,证明△BCF∽△ECG,△ACG∽△HCF,可得比例线段,则结论得证.
解:(1)∵AD、AE分别是△ABC中∠A内角的平分线和外角平分线,
∴∠DAE=∠DAC+∠EAC
=![]() ∠BAC+
∠BAC+![]() ∠CAF
∠CAF
=![]() (∠BAC+∠CAF)
(∠BAC+∠CAF)
=![]() ×180°=90°.
×180°=90°.
故答案为:90°;
(2)证明:过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,如图1,
,如图1,
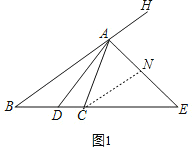
则有![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ;
;
(3)如图2,分别延长![]() 、
、![]() 交于点
交于点![]() ;
;
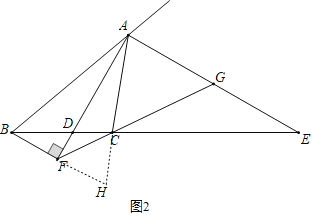
![]() 为
为![]() 的角平分线,
的角平分线,
![]() ;
;
在![]() 与
与![]() 中,
中,
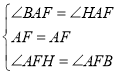 ,
,
![]() ,
,
![]() ;
;
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
∵![]() ,
,
![]() .
.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:初中数学 来源: 题型:
【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.下列叙述正确的是( )

A. 小球的飞行高度不能达到15m
B. 小球的飞行高度可以达到25m
C. 小球从飞出到落地要用时4s
D. 小球飞出1s时的飞行高度为10m
查看答案和解析>>
科目:初中数学 来源: 题型:
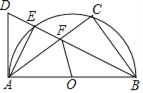
【题目】如图,以AB为直径作半圆O,点C是半圆上一点,∠ABC的平分线交⊙O于E,D为BE延长线上一点,且∠DAE=∠FAE.
(1)求证:AD为⊙O切线;
(2)若sin∠BAC=![]() ,求tan∠AFO的值.
,求tan∠AFO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数图象的顶点在原点![]() ,对称轴为
,对称轴为![]() 轴.一次函数
轴.一次函数![]() 的图象与二次函数的图象交于
的图象与二次函数的图象交于![]() 两点(
两点(![]() 在
在![]() 的左侧),且
的左侧),且![]() 点坐标为
点坐标为![]() .平行于
.平行于![]() 轴的直线
轴的直线![]() 过
过![]() 点.
点.
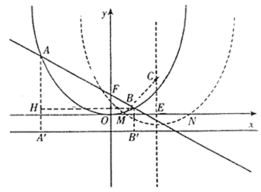
(1)求一次函数与二次函数的解析式;
(2)判断以线段AB为直径的圆与直线![]() 的位置关系,并给出证明;
的位置关系,并给出证明;
(3)把二次函数的图象向右平移 2 个单位,再向下平移 t 个单位(t>0),二次函数的图象与x 轴交于 M,N 两点,一次函数图象交y 轴于 F 点.当 t 为何值时,过 F,M,N 三点的圆的面积最小?最小面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”,自行车成为人们喜爱的交通工具.某品牌共享自行车在温州的投放量自2017年起逐月增加,据统计,该品牌共享自行车1月份投放了640辆,3月份投放了1000辆.
(1)该品牌共享自行车前3个月的投放量的月平均增长率相同,则这三个月一共投放了多少辆自行车?
(2)考虑到增强客户体验,该品牌共享自行车准备投入3万元向自行车生产厂商定制了一批两种规格比较高档的自行车,之后投放到某高端写字楼区域.已知自行车生产厂商生产A型车的成本价为300元/辆,售价为500元/辆,生产B型车的成本价为700元/辆,售价为1000元/辆.根据指定要求,B型车的数量需超过12辆,且A型车的数量不少于B型车的2倍.自行车生产厂商应如何设计生产方案才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
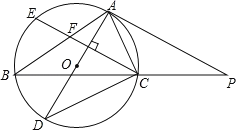
【题目】如图,AD是△ABC的外接圆⊙O的直径,点P在BC延长线上,PA是⊙O的切线,且∠B=35°.
(1)求∠PAC的度数.
(2)弦CE⊥AD交AB于点F,若AFAB=12,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影.已知桌面的直径为1.2 m,桌面距离地面1 m.若灯泡距离地面3 m,则地面上阴影部分的面积为 ( )

A. 0.36πm2 B. 0.81πm2 C. 2πm2 D. 3.24πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知边长为4的正方形钢板有一个角锈蚀,其中AF=2,BF=1,为了合理利用这块钢板.将在五边形EABCD内截取一个矩形块MDNP,使点P在AB上,且要求面积最大,求钢板的最大利用率.
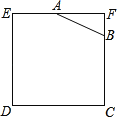
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com