

分析 (1)13层时最底层最左边这个圆圈中的数是第12层的最后一个数加1;
(2)首先计算圆圈的个数,用-23+数的个数减去1就是最底层最右边圆圈内的数;
(3)利用(2)把所有数的绝对值相加即可.
解答 解:(1)当有13层时,图3中到第12层共有:1+2+3+…+11+12=78个圆圈,
最底层最左边这个圆圈中的数是:78+1=79;
(2)图4中所有圆圈中共有1+2+3+…+13=$\frac{13×14}{2}$=91个数,
最底层最右边圆圈内的数是-23+91-1=67;
(3)图4中共有91个数,其中23个负数,1个0,67个正数,
所以图4中所有圆圈中各数的和为:
|-23|+|-22|+…+|-1|+0+1+2+…+67
=(1+2+3+…+23)+(1+2+3+…+67)
=276+2278
=2554.
故答案为:(1)79;(2)67.
点评 此题主要考查了图形的变化类,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.注意连续整数相加的时候的这种简便计算方法.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:解答题
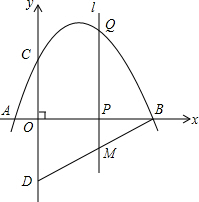 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A、点B,与y轴交于点C、点D与点C关于x轴对称,点P是x轴上一动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2与x轴交于点A、点B,与y轴交于点C、点D与点C关于x轴对称,点P是x轴上一动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,弦AD平分∠CAB,过点D作DE⊥AC,垂足为点E,ED的延长线交AB的延长线于点F.
如图,AB为⊙O的直径,弦AD平分∠CAB,过点D作DE⊥AC,垂足为点E,ED的延长线交AB的延长线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com