
【题目】如图,方格纸上的每个小方格都是边长为1的正方形,△ABC 的顶点均在格点上,若 B
点的坐标为(-4,-2), 按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点A和点C的坐标;
(3)画出△ABC关于x轴的对称图形△ABC;
(4)△ABC 的面积为________.

科目:初中数学 来源: 题型:
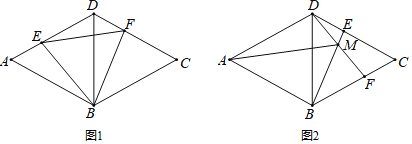
【题目】如图,已知菱形ABCD边长为4,![]() ,点E从点A出发沿着AD、DC方向运动,同时点F从点D出发以相同的速度沿着DC、CB的方向运动.
,点E从点A出发沿着AD、DC方向运动,同时点F从点D出发以相同的速度沿着DC、CB的方向运动.
![]() 如图1,当点E在AD上时,连接BE、BF,试探究BE与BF的数量关系,并证明你的结论;
如图1,当点E在AD上时,连接BE、BF,试探究BE与BF的数量关系,并证明你的结论;
![]() 在
在![]() 的前提下,求EF的最小值和此时
的前提下,求EF的最小值和此时![]() 的面积;
的面积;
![]() 当点E运动到DC边上时,如图2,连接BE、DF,交点为点M,连接AM,则
当点E运动到DC边上时,如图2,连接BE、DF,交点为点M,连接AM,则![]() 大小是否变化?请说明理由.
大小是否变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平移线段AB,使点A移动到点A1.
(1)画出平移后的线段A1B1,分别连接AA1,BB1.
(2)分别画出AC⊥A1B1于点C,AD⊥BB1于点D.
(3)AA1与BB1之间的距离,就是线段 的长度.
(4)线段AB平移的距离,就是线段 的长度.
(5)线段BD的长度,是点B到直线 的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y= ![]() x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )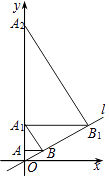
A.(0,42015)
B.(0,42014)
C.(0,32015)
D.(0,32014)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=_____°,射线OC的方向是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车以汽车站为出发点,在东西方向的城市道路上进行营运,若规定向东为正,向西为负,行车依先后顺序记录如下(单位:千米):
+4,-5,+9,-3,+6,-3,-8,-4,+7,-6.
(1)计算说明出租车将最后一名乘客送到目的地,此时离汽车站多远?在汽车站什么方向?
(2)若该出租车每千米收费标准为3元,求出租车的营业额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,点B和点C分别是x轴的正半轴和y轴的正半轴上的两点,且OB:BC=1:![]() ,直线BC的解析式为y=﹣kx+6k(k≠0).
,直线BC的解析式为y=﹣kx+6k(k≠0).
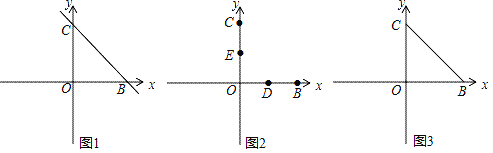
(1)如图1,求点C的坐标;
(2)如图2,点D为OB中点,点E为OC中点,点F在y轴的负半轴上,点A是射线FD上的第一象限的点,连接AE、ED,若FD=DA,且S△AED=![]() ,求点A的坐标;
,求点A的坐标;
(3)如图3,在(2)的条件下,点P在线段OB上,点Q在线段OC的延长线上,CQ=BP,连接PQ与BC交于点M,连接AM并延长AM到点N,连接QN、AP、AB和NP,若∠QPA﹣∠NQO=∠NQP﹣∠PAB,NP=2![]() ,求直线PQ的解析式.
,求直线PQ的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司一共62辆![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人/辆 | 380元/辆 |
| 20人/辆 | 280元/辆 |
注:载客量指的是每辆客车最多可载该校师生的人数.设学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案总费用最省?最省的总费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com