
ЁОЬтФПЁПЙцЖЈЃКВЛЯрНЛЕФСНИіКЏЪ§ЭМЯѓдкЪњжБЗНЯђЩЯЕФзюЖЬОрРыЮЊетСНИіКЏЪ§ЕФЁАЧзНќОрРыЁБ
ЃЈ1ЃЉЧѓХзЮяЯпyЃНx2Љ2x+3гыxжсЕФЁАЧзНќОрРыЁБЃЛ
ЃЈ2ЃЉдкЬНОПЮЪЬтЃКЧѓХзЮяЯпyЃНx2Љ2x+3гыжБЯпyЃНxЉ1ЕФЁАЧзНќОрРыЁБЕФЙ§ГЬжаЃЌгаШЫЬсГіЃКЙ§ХзЮяЯпЕФЖЅЕуЯђxжсзїДЙЯпгыжБЯпЯрНЛЃЌдђИУЮЪЬтЕФЁАЧзНќОрРыЁБвЛЖЈЪЧХзЮяЯпЖЅЕугыНЛЕужЎМфЕФОрРыЃЌФуЭЌвтЫћЕФПДЗЈТ№ЃПЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШєХзЮяЯпyЃНx2Љ2x+3гыХзЮяЯпyЃН![]() +cЕФЁАЧзНќОрРыЁБЮЊ
+cЕФЁАЧзНќОрРыЁБЮЊ![]() ЃЌЧѓcЕФжЕЃЎ
ЃЌЧѓcЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2ЃЛЃЈ2ЃЉВЛЭЌвтЫћЕФПДЗЈЃЌРэгЩЯъМћНтЮіЃЛЃЈ3ЃЉcЃН1ЃЎ
ЁОНтЮіЁП
(1)Абy=x2Љ2x+3ХфГЩЖЅЕуЪНЕУЕНХзЮяЯпЩЯЕФЕуЕНxжсЕФзюЖЬОрРыЃЌШЛКѓИљОнЬтвтНтОіЮЪЬтЃЛ
(2)ШчЭМЃЌPЕуЮЊХзЮяЯпy=x2Љ2x+3ШЮвтвЛЕуЃЌзїPQЁЮyжсНЛжБЯпy=xЉ1гкQЃЌЩшP(tЃЌt2Љ2t+3)ЃЌдђQ(tЃЌtЉ1)ЃЌдђPQ=t2Љ2t+3Љ(tЉ1)ЃЌШЛКѓРћгУЖўДЮКЏЪ§ЕФаджЪЕУЕНХзЮяЯпy=x2Љ2x+3гыжБЯпy=xЉ1ЕФЁАЧзНќОрРыЁБЃЌШЛКѓЖдЫћЕФПДЗЈНјааХаЖЯЃЛ
(3)MЕуЮЊХзЮяЯпy=x2Љ2x+3ШЮвтвЛЕуЃЌзїMNЁЮyжсНЛХзЮяЯп![]() гкNЃЌЩшM(tЃЌt2Љ2t+3)ЃЌдђN(tЃЌ
гкNЃЌЩшM(tЃЌt2Љ2t+3)ЃЌдђN(tЃЌ![]() t2+c)ЃЌгы(2)ЗНЗЈвЛбљЕУЕНMNЕФзюаЁжЕЮЊ
t2+c)ЃЌгы(2)ЗНЗЈвЛбљЕУЕНMNЕФзюаЁжЕЮЊ![]() ЉcЃЌДгЖјЕУЕНХзЮяЯпy=x2Љ2x+3гыХзЮяЯп
ЉcЃЌДгЖјЕУЕНХзЮяЯпy=x2Љ2x+3гыХзЮяЯп![]() ЕФЁАЧзНќОрРыЁБЃЌЫљвд
ЕФЁАЧзНќОрРыЁБЃЌЫљвд![]() ЃЌШЛКѓНтЗНГЬМДПЩЃЎ
ЃЌШЛКѓНтЗНГЬМДПЩЃЎ
(1)Ёпy=x2Љ2x+3=(xЉ1)2+2ЃЌ
ЁрХзЮяЯпЩЯЕФЕуЕНxжсЕФзюЖЬОрРыЮЊ2ЃЌ
ЁрХзЮяЯпy=x2Љ2x+3гыxжсЕФЁАЧзНќОрРыЁБЮЊЃК2ЃЛ
(2)ВЛЭЌвтЫћЕФПДЗЈЃЎРэгЩШчЯТЃК
ШчЭМЃЌPЕуЮЊХзЮяЯпy=x2Љ2x+3ШЮвтвЛЕуЃЌзїPQЁЮyжсНЛжБЯпy=xЉ1гкQЃЌ
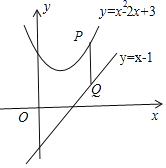
ЩшP(tЃЌt2Љ2t+3)ЃЌдђQ(tЃЌtЉ1)ЃЌ
ЁрPQ=t2Љ2t+3Љ(tЉ1)=t2Љ3t+4=(tЉ![]() )2+
)2+![]() ЃЌ
ЃЌ
ЕБt=![]() ЪБЃЌPQгазюаЁжЕЃЌзюаЁжЕЮЊ
ЪБЃЌPQгазюаЁжЕЃЌзюаЁжЕЮЊ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпy=x2Љ2x+3гыжБЯпy=xЉ1ЕФЁАЧзНќОрРыЁБЮЊ![]() ЃЌ
ЃЌ
ЖјЙ§ХзЮяЯпЕФЖЅЕуЯђxжсзїДЙЯпгыжБЯпЯрНЛЃЌХзЮяЯпЖЅЕугыНЛЕужЎМфЕФОрРыЮЊ2ЃЌ
ЁрВЛЭЌвтЫћЕФПДЗЈЃЛ
(3)MЕуЮЊХзЮяЯпy=x2Љ2x+3ШЮвтвЛЕуЃЌзїMNЁЮyжсНЛХзЮяЯп![]() гкNЃЌ
гкNЃЌ

ЩшM(tЃЌt2Љ2t+3)ЃЌдђN(tЃЌ![]() t2+c)ЃЌ
t2+c)ЃЌ
ЁрMN=t2Љ2t+3Љ(![]() t2+c)=
t2+c)=![]() t2Љ2t+3Љc=
t2Љ2t+3Љc=![]() (tЉ
(tЉ![]() )2+
)2+![]() ЉcЃЌ
ЉcЃЌ
ЕБt=![]() ЪБЃЌMNгазюаЁжЕЃЌзюаЁжЕЮЊ
ЪБЃЌMNгазюаЁжЕЃЌзюаЁжЕЮЊ![]() ЉcЃЌ
ЉcЃЌ
ЁрХзЮяЯпy=x2Љ2x+3гыХзЮяЯп![]() ЕФЁАЧзНќОрРыЁБЮЊ
ЕФЁАЧзНќОрРыЁБЮЊ![]() ЉcЃЌ
ЉcЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрc=1ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛМвЪпВЫЙЋЫОМЦЛЎЕНФГТЬЩЋЪпВЫЛљЕиЪеЙКAЃЌBСНжжЪпВЫЙВ140ЖжЃЌдЄМЦСНжжЪпВЫЯњЪлКѓЛёРћЕФЧщПіШчЯТБэЫљЪОЃК
ЯњЪлЦЗжж | AжжЪпВЫ | BжжЪпВЫ |
УПЖжЛёРћ(дЊ) | 1200 | 1000 |
ЦфжаAжжЪпВЫЕФ5%ЃЌBжжЪпВЫЕФ3%аыдЫЭљCЪаГЁЯњЪлЃЌЕЋCЪаГЁЕФЯњЪлзмСПВЛГЌЙ§5.8ЖжЃЎЩшЯњЪлРћШѓЮЊWдЊ(ВЛМЦЫ№КФ)ЃЌЙКНјAжжЪпВЫxЖжЃЎ
ЃЈ1ЃЉЧѓWгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉНЋет140ЖжЪпВЫШЋВПЯњЪлЭъЃЌзюЖрПЩЛёЕУЖрЩйРћШѓЃП
ЃЈ3ЃЉгЩгкЪмЪаГЁвђЫигАЯьЃЌЙЋЫОНјЛѕЪБЕїВщЗЂЯжЃЌAжжЪпВЫУПЖжПЩЖрЛёРћ100дЊЃЌBжжЪпВЫУПЖжПЩЖрЛёРћm(200ЃМmЃМ400)дЊЃЌЕЋBжжЪпВЫЯњЪлЪ§СПВЛГЌЙ§90ЖжЃЎЙЋЫОЩшМЦСЫвЛжжЛёРћзюДѓЕФНјЛѕЗНАИЃЌЯњЪлЭъКѓПЩЛёРћ179000дЊЃЌЧѓmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAЃЌBЪЧЗДБШР§КЏЪ§y=![]() дкЕквЛЯѓЯоФкЕФЭМЯѓЩЯЕФСНЕуЃЌЧвAЃЌBСНЕуЕФКсзјБъЗжБ№ЪЧ2КЭ4ЃЌдђЁїOABЕФУцЛ§ЪЧЃЈЁЁЁЁЃЉ
дкЕквЛЯѓЯоФкЕФЭМЯѓЩЯЕФСНЕуЃЌЧвAЃЌBСНЕуЕФКсзјБъЗжБ№ЪЧ2КЭ4ЃЌдђЁїOABЕФУцЛ§ЪЧЃЈЁЁЁЁЃЉ
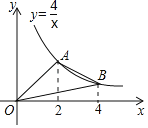
A. 4 B. 3 C. 2 D. 1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
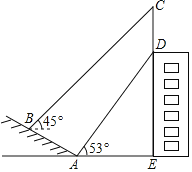
ЁОЬтФПЁПНЬг§ВПВМЕФЁЖЛљДЁНЬг§ПЮГЬИФИяИйвЊЁЗвЊЧѓУПЮЛбЇЩњУПбЇФъЖМвЊВЮМгЩчЛсЪЕМљЛюЖЏЃЌФГбЇаЃзщжЏСЫвЛДЮВтСПЬНОПЛюЖЏЃЌШчЭМЃЌФГДѓТЅЕФЖЅВПЪњгавЛПщЙуИцХЦCDЃЌаЁУїгыЭЌбЇУЧдкЩНЦТЕФЦТНХAДІВтЕУЙуИцХЦЕзВПDЕФбіНЧЮЊ53ЁуЃЌбиЦТУцABЯђЩЯзпЕНBДІВтЕУЙуИцХЦЖЅВПCЕФбіНЧЮЊ45ЁуЃЌвбжЊЩНЦТABЕФЦТЖШ1ЃК![]() ЃЌABЃН10УзЃЌAEЃН21УзЃЌЧѓЙуИцХЦCDЕФИпЖШЃЎЃЈВтНЧЦїЕФИпЖШКіТдВЛМЦЃЌНсЙћОЋШЗЕН0.1УзЃЌВЮПМЪ§ОнЃК
ЃЌABЃН10УзЃЌAEЃН21УзЃЌЧѓЙуИцХЦCDЕФИпЖШЃЎЃЈВтНЧЦїЕФИпЖШКіТдВЛМЦЃЌНсЙћОЋШЗЕН0.1УзЃЌВЮПМЪ§ОнЃК![]() Ёж1.41ЃЌ
Ёж1.41ЃЌ![]() Ёж1.73ЃЌtan53ЁуЁж
Ёж1.73ЃЌtan53ЁуЁж![]() ЃЌcos53ЁуЁж0.60ЃЉ
ЃЌcos53ЁуЁж0.60ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЫФБпаЮOACBЪЧСтаЮЃЌOBдкXжсЕФе§АыжсЩЯЃЌsinЁЯAOB=![]() ЃЎЗДБШР§КЏЪ§y=
ЃЎЗДБШР§КЏЪ§y=![]() дкЕквЛЯѓЯоЭМЯѓОЙ§ЕуAЃЌгыBCНЛгкЕуFЃЎSЁїAOF=
дкЕквЛЯѓЯоЭМЯѓОЙ§ЕуAЃЌгыBCНЛгкЕуFЃЎSЁїAOF=![]() ЃЌдђk=ЃЈЁЁЁЁЃЉ
ЃЌдђk=ЃЈЁЁЁЁЃЉ

A. 15 B. 13 C. 12 D. 5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
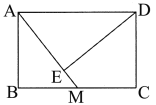
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌAB=4ЃЌBC=6ЃЌMЪЧBCЕФжаЕуЃЌDE![]() AMЃЌEЮЊДЙзуЃЎ
AMЃЌEЮЊДЙзуЃЎ
ЃЈ1ЃЉжЄУїЃКЁїABMЁзЁїDEAЃЛ
ЃЈ2ЃЉЧѓЁїADEЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
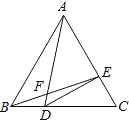
ЁОЬтФПЁПШчЭМЃЌЁїABC ЪЧЕШБпШ§НЧаЮЃЌЕу DЁЂE ЗжБ№дк BCЁЂAC ЩЯЃЌЧв BD=![]() BCЃЌCE=
BCЃЌCE= ![]() ACЃЌBEЁЂAD ЯрНЛгкЕу FЃЌСЌНг DEЃЌ дђЯТСаНсТлЃКЂйЁЯAFE=60ЁуЃЛЂкDEЁЭACЃЛЂлCE2=DFDAЃЛЂмAFBE=AEACЃЌе§ШЗЕФНсТлгаЃЈ ЃЉ
ACЃЌBEЁЂAD ЯрНЛгкЕу FЃЌСЌНг DEЃЌ дђЯТСаНсТлЃКЂйЁЯAFE=60ЁуЃЛЂкDEЁЭACЃЛЂлCE2=DFDAЃЛЂмAFBE=AEACЃЌе§ШЗЕФНсТлгаЃЈ ЃЉ
A.ЂйЂкЂлB.ЂйЂкЂмC.ЂйЂлЂмD.ЂйЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
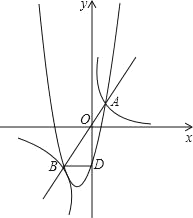
ЁОЬтФПЁПШчЭМЃЌжБНЧзјБъЯЕжаyЃНmxКЭ![]() ЃЈmЃО0ЃЉЭМЯѓЕФНЛЕуЮЊAЁЂBЃЌBDЁЭyжсгкDЃЌSЁїABDЃН4ЃЛжБЯпAЁфBЁфгЩжБЯпABЛКТ§ЯђЯТЦНвЦЃЛ
ЃЈmЃО0ЃЉЭМЯѓЕФНЛЕуЮЊAЁЂBЃЌBDЁЭyжсгкDЃЌSЁїABDЃН4ЃЛжБЯпAЁфBЁфгЩжБЯпABЛКТ§ЯђЯТЦНвЦЃЛ
ЃЈ1ЃЉЧѓmЕФжЕЃЛ
ЃЈ2ЃЉЮЪжБЯпAЁфBЁфЯђЯТЦНвЦЖрЩйЕЅЮЛЪБгыОЙ§BЁЂDЁЂAШ§ЕуЕФХзЮяЯпИеКУжЛгавЛИіНЛЕуЃЌВЂЧѓГіНЛЕузјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХЛЅСЊЭјЕФВЛЖЯЗЂеЙЃЌвЦЖЏжЇИЖЕФЦеМАТЪдНРДдНИпЃЌШЫУЧдкЙКЮяЪБПЩбЁдёЕФИЖПюЗНЪНдНРДдНЖрбљЛЏЃЎЮЊСЫНтШЫУЧЙКЮяЪБГЃгУИЖПюЗНЪНЃЌдкФГВНааНжНјааСЫЫцЛњГщбљЕїВщЃЌИљОнЕїВщНсЙћЛцжЦвдЯТСНЗљВЛЭъећЭГМЦЭМЃЌЧыНсКЯЭМжаЫљИјаХЯЂНтД№ЯТСаЮЪЬтЃК
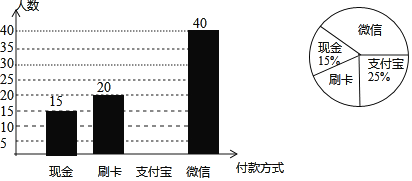
ЃЈ1ЃЉДЫДЮЙВЕїВщСЫЁЁ ЁЁШЫЃЌБэЪОГЃгУЁАЮЂаХЁБИЖПюЗНЪНЕФЩШаЮдВаФНЧЖШЪ§ЮЊЁЁ ЁЁЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ2ЃЉИУВНааНжФГЬьЕФШЫСїСПдМЮЊ2.4ЭђШЫЃЌЦфжадМга50%ЕФШЫВЮгыЙКЮяЃЌИљОнЕїВщЛёЕУЕФаХЯЂЃЌЙРМЦдкетвЛЬьЙКЮяЪБгУЁАЮЂаХЁБИЖПюЗНЪНЕФШЫЪ§ЮЊЖрЩйЭђШЫЃП
ЃЈ3ЃЉШєМзЁЂввСНШЫдкЙКЮяЪБЃЌбЁдёЁАЯжН№ЁБЁЂЁАЫЂПЈЁБЁЂЁАжЇИЖБІЁБЁЂЁАЮЂаХЁБЃЈЗжБ№гУAЁЂBЁЂCЁЂDБэЪОЃЉИЖПюЕФПЩФмадЯрЭЌЃЎЧыЭЈЙ§СаБэЛђЛЪїаЮЭМЕФЗНЗЈЃЌЧѓСНШЫдкЙКЮяЪБЃЌгУЭЌвЛжжИЖПюЗНЪНЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com