
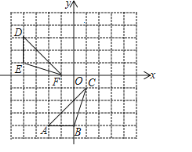
【题目】如图,△ABC和△DEF的顶点都在格点上,请解答下列问题:
(1) 画出△ABC绕点O逆时针旋转90°后的图形△A1B1C1,A、B、C的对应点分别是A1、B1、C1
(2) 设(1)中的线段A A1与线段B B1的长分别为a和b,则![]() ___________
___________
(3) △A1B1C1与△DEF关于某点对称,请直接写出它们对称中心的坐标.
科目:初中数学 来源: 题型:
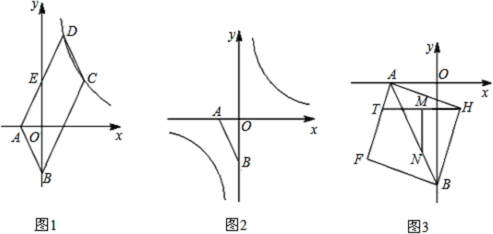
【题目】如图1,已知点![]() ,
,![]() ,且
,且![]() 、
、![]() 满足
满足![]() ,
,![]() 的边
的边![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() 为
为![]() 中点,双曲线
中点,双曲线![]() 经过
经过![]() 、
、![]() 两点.
两点.
(1)求![]() 的值;
的值;
(2)点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 在
在![]() 轴上,若以点
轴上,若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,试求满足要求的所有点
为顶点的四边形是平行四边形,试求满足要求的所有点![]() 、
、![]() 的坐标;
的坐标;
(3)以线段![]() 为对角线作正方形
为对角线作正方形![]() (如图
(如图![]() ,点
,点![]() 是边
是边![]() 上一动点,
上一动点,![]() 是
是![]() 的中点,
的中点,![]() ,交
,交![]() 于
于![]() ,当
,当![]() 在
在![]() 上运动时,
上运动时,![]() 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B两地.甲、乙两人同时出发,甲骑电动车从A地到B地,中途出现故障后停车维修,修好车后以原速继续行驶到B地;乙骑摩托车从B地到A地,到达A地后立即按原原速返回,结果两人同时到B地.如图是甲、乙两人与B地的距离y(km)与乙行驶时间x(h)之间的函数图象.
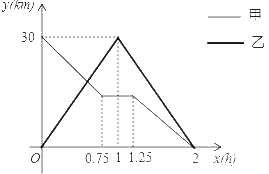
(1)A、B两地间的距离为 km;
(2)求乙与B地的距离y(km)与乙行驶时间x(h)之间的函数关系式;
(3)求甲、乙第一次相遇的时间;
(4)若两人之间的距离不超过10km时,能够用无线对讲机保持联系,请求出乙在行进中能用无线对讲机与甲保持联系的x取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行以“助人为乐,乐在其中”为主题的演讲比赛,比赛设一个第一名,一个第二名,两个并列第三名.前四名中七、八年级各有一名同学,九年级有两名同学,小蒙同学认为前两名是九年级同学的概率是![]() ,你赞成他的观点吗?请用列表法或画树形图法分析说明.
,你赞成他的观点吗?请用列表法或画树形图法分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
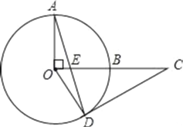
【题目】如图,OA、OB是⊙O的半径,OA⊥OB,C为OB延长线上一点,CD切⊙O于点D,E为AD与OC的交点,连接OD.已知CE=5,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一个六面分别标有数字1,2,3,4,5,6,且质地均匀的正方体筛子,另有三张正面分别标有1,2,3,的卡片(卡片除数字外,其他都相同),先由小明掷筛子一次,记下筛子向上一面出现的数字,然后由小王从三张背面朝上放置在桌面上的卡片中随机抽取一张,记下卡片上的数字。
(1)请用列表或树状图的方法,求出筛子向上一面出现的数字与卡片上的数字之积为6的概率;
(2)小明和小王做游戏,约定游戏规则如下:若筛子向上一面出现的数字与卡片上的数字之积大于7,则小明赢;若筛子向上一面出现的数字与卡片上的数字之积小于7,则小王赢;问小明和小王谁赢的可能性更大?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D是抛物线的顶点.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D是抛物线的顶点.
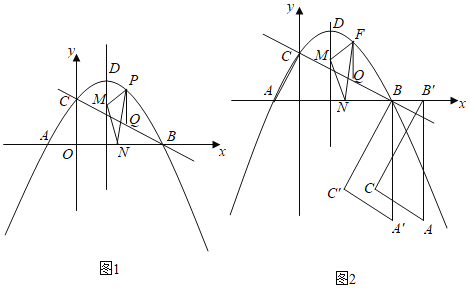
(1)如图1,P为直线BC上方抛物线上一动点,过点P作PQ∥y轴交BC于点Q.在抛物线的对称轴上有一动点M,在x轴上有一动点N,当6PQ﹣CQ的值最大时,求PM+MN+![]() NB的最小值;
NB的最小值;
(2)如图2,将△ABC绕点B逆时针旋转90°后得到△A′BC',再将△A′BC′向右平移1个单位得到△A“B′C“,那么在抛物线的对称轴DM上,是否存在点T,使得△A′B′T为等腰三角形?若存在,求出点T到x轴的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=3,点E、F分别在AC,AB上,连接EF.
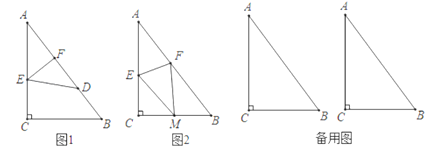
(1)将△ABC沿EF折叠,使点A落在AB边上的点D处,如图1,若S四边形ECBD=2S△EDF,求AE的长;
(2)将△ABC沿EF折叠,使点A落在BC边上的点M处,如图2,若MF⊥CB.
①求AE的长;②求四边形AEMF的面积;
(3)若点E在射线AC上,点F在边AB上,点A关于EF所在直线的对称点为点P,问:是否存在以PF、CB为对边的平行四边形,若存在,求出AE的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com