
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D是抛物线的顶点.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D是抛物线的顶点.
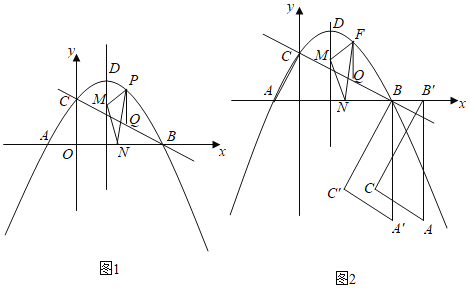
(1)如图1,P为直线BC上方抛物线上一动点,过点P作PQ∥y轴交BC于点Q.在抛物线的对称轴上有一动点M,在x轴上有一动点N,当6PQ﹣CQ的值最大时,求PM+MN+![]() NB的最小值;
NB的最小值;
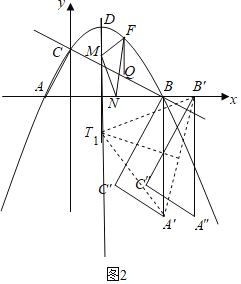
(2)如图2,将△ABC绕点B逆时针旋转90°后得到△A′BC',再将△A′BC′向右平移1个单位得到△A“B′C“,那么在抛物线的对称轴DM上,是否存在点T,使得△A′B′T为等腰三角形?若存在,求出点T到x轴的距离;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在.T到x轴的距离为
;(2)存在.T到x轴的距离为![]() 或4﹣
或4﹣![]() 或4+
或4+![]() 或2
或2![]() .
.
【解析】
(1)令x=0得到C(0,![]() ),令y=0得到A(﹣1,0),B(3,0),BC=2
),令y=0得到A(﹣1,0),B(3,0),BC=2![]() ,设直线BC解析式为y=kx+b,计算得到直线BC解析式为y=﹣
,设直线BC解析式为y=kx+b,计算得到直线BC解析式为y=﹣![]() x+
x+![]() ,设P(m,﹣
,设P(m,﹣![]() m2+
m2+![]() m+
m+![]() ),由题意得到BK=
),由题意得到BK=![]() ;过P′作P′T⊥BK于T,作P′W∥y轴交BK于点W,根据三角函数得到NT=
;过P′作P′T⊥BK于T,作P′W∥y轴交BK于点W,根据三角函数得到NT=![]() NB;由B(3,0),K(0,﹣
NB;由B(3,0),K(0,﹣![]() ),则直线BK解析式为y=
),则直线BK解析式为y=![]() x
x![]() ,根据平行线的性质及相似三角形的判定得到△P′WT∽△BKO,由相似三角形的性质结合题意进行计算,得到答案;
,根据平行线的性质及相似三角形的判定得到△P′WT∽△BKO,由相似三角形的性质结合题意进行计算,得到答案;
(2)由旋转的性质得到A′(3,﹣4),B′(4,0),设T(1,t),由于△A′B′T为等腰三角形,所以分三种情形:①A′T=B′T;②A′T=A′B′;③B′T=A′B′,进行计算,即可得到答案.
解:(1)在抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 中,令x=0,得y=
中,令x=0,得y=![]() ,∴C(0,
,∴C(0,![]() ),
),
令y=0,得0=﹣![]() x2+
x2+![]() x+
x+![]() ,解得x1=﹣1,x2=3,∴A(﹣1,0),B(3,0),BC=2
,解得x1=﹣1,x2=3,∴A(﹣1,0),B(3,0),BC=2![]() ,
,
设直线BC解析式为y=kx+b,则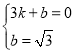 ,解得
,解得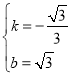 ,
,
∴直线BC解析式为y=﹣![]() x+
x+![]() ,
,
设P(m,﹣![]() m2+
m2+![]() m+
m+![]() ),则Q(m,﹣
),则Q(m,﹣![]() m+
m+![]() ),PQ=﹣
),PQ=﹣![]() m2+
m2+![]() m,CQ=
m,CQ=![]() m
m
∴6PQ﹣CQ=6(﹣![]() m2+
m2+![]() m)﹣
m)﹣![]() m=﹣2
m=﹣2![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
∵﹣2![]() <0,∴当m=
<0,∴当m=![]() 时,6PQ﹣CQ的值最大,此时,P(
时,6PQ﹣CQ的值最大,此时,P(![]() ,
,![]() ),
),
由y=﹣![]() x2+
x2+![]() x+
x+![]() =-
=-![]() (x﹣1)2+
(x﹣1)2+![]() ,得抛物线对称轴为:x=1,
,得抛物线对称轴为:x=1,
作点P关于对称轴x=1的对称点P′(![]() ,
,![]() ),在y轴负半轴上取点K(0,﹣
),在y轴负半轴上取点K(0,﹣![]() ),连接BK交对称轴于S,则BK=
),连接BK交对称轴于S,则BK=![]() ,
,
过P′作P′T⊥BK于T,作P′W∥y轴交BK于点W,
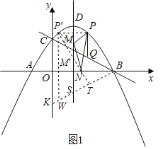
在△BNT中,![]() =tan∠OBK=
=tan∠OBK=![]() ,∴NT=
,∴NT=![]() NB,
NB,
∴线段P′T长度为PM+MN+![]() NB最小值,
NB最小值,
∵B(3,0),K(0,﹣![]() ),∴直线BK解析式为y=
),∴直线BK解析式为y=![]() x
x![]() ,
,
∴W(![]() ,
,![]() ),P′W=
),P′W=![]() ﹣(
﹣(![]() )=
)=![]() ,
,
∵P′W∥y轴,∴∠P′WT=∠BKO
∵∠P′TW=∠BOK=90°
∴△P′WT∽△BKO
∴![]() ,P′T=
,P′T=![]() ×
×![]() =
=![]() ,
,
∴PM+MN+![]() NB最小值=
NB最小值=![]() .
.
(2)存在.
∵△ABC绕点B逆时针旋转90°后得到△A′BC',再将△A′BC′向右平移1个单位得到△A′′B′C′′,
∴A′(3,﹣4),B′(4,0),∵点T在抛物线对称轴直线x=1上,∴设T(1,t)
∵△A′B′T为等腰三角形,∴分三种情形:
①A′T=B′T,(3﹣1)2+(﹣4﹣t)2=(4﹣1)2+(0﹣t)2,解得:t=![]() ,
,
∴此时T到x轴的距离为![]() ;
;
②A′T=A′B′,(3﹣1)2+(﹣4﹣t)2=(3﹣4)2+(﹣4﹣0)2,解得:t=﹣4+![]() 或﹣4﹣
或﹣4﹣![]() ,
,
∴此时T到x轴的距离为4﹣![]() 或4+
或4+![]() ;
;
③B′T=A′B′,(4﹣1)2+(0﹣t)2=(3﹣4)2+(﹣4﹣0)2,解得:t=2![]() 或﹣2
或﹣2![]() ,
,
∴此时T到x轴的距离为2![]() ;
;
综上所述,T到x轴的距离为![]() 或4﹣
或4﹣![]() 或4+
或4+![]() 或2
或2![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
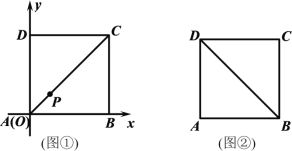
【题目】已知动点P在边长为1的正方形ABCD的内部,点P到边AD、AB的距离分别为m、n.
(1)以A为原点,以边AB所在直线为x轴,建立平面直角坐标系,如图①所示,当点P在对角线AC上,且m=![]() 时,求点P的坐标;
时,求点P的坐标;
(2)如图②,当m、n满足什么条件时,点P在△DAB的内部?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
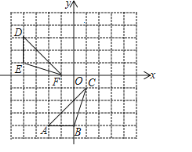
【题目】如图,△ABC和△DEF的顶点都在格点上,请解答下列问题:
(1) 画出△ABC绕点O逆时针旋转90°后的图形△A1B1C1,A、B、C的对应点分别是A1、B1、C1
(2) 设(1)中的线段A A1与线段B B1的长分别为a和b,则![]() ___________
___________
(3) △A1B1C1与△DEF关于某点对称,请直接写出它们对称中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】休闲广场的边缘是一个坡度为i=1:2.5的缓坡CD,靠近广场边缘有一架秋千.秋千静止时,底端A到地面的距离AB=0.5m,B到缓坡底端C的距离BC=0.7m.若秋千的长OA=2m,则当秋千摆动到与静止位置成37°时,底端A′到坡面的竖直方向的距离A′E约为( )(参考数据:sin37°=0.60,cos37°=0.80,tan37°=0.75)
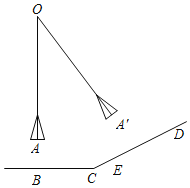
A. 0.4mB. 0.5mC. 0.6mD. 0.7m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击选示在10次射击训练中的成绩统计图(部分)如图所示:

根据以上信息,请解答下面的问题;
选手 | A平均数 | 中位数 | 众数 | 方差 |
甲 | a | 8 | 8 | c |
乙 | 7.5 | b | 6和9 | 2.65 |
(1)补全甲选手10次成绩频数分布图.
(2)a= ,b= ,c= .
(3)教练根据两名选手手的10次成绩,决定选甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(3)班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
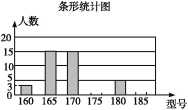
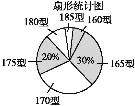
根据以上信息,解答下列问题:
(1)该班共有多少名学生?其中穿175型校服的学生有多少人?
(2)在条形统计图中,请把空缺的部分补充完整;
(3)在扇形统计图中,请计算185型校服所对应扇形圆心角的大小;
(4)求该班学生所穿校服型号的众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
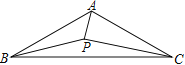
【题目】如图,△ABC中,AB=AC,点P为△ABC内一点,∠APB=∠BAC=120°.若AP+BP=4,则PC的最小值为( )
A. 2B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
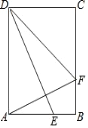
【题目】在矩形ABCD中,BC=10cm、DC=6cm,点E、F分别为边AB、BC上的两个动点,E从点A出发以每秒5cm的速度向B运动,F从点B出发以每秒3cm的速度向C运动,设运动时间为t秒.若∠AFD=∠AED,则t的值为( )
A. ![]() B. 0.5C.
B. 0.5C. ![]() D. 1
D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com