【题目】对于二次函数
，下列说法正确的个数是（ ）
①对于任何满足条件的
，该二次函数的图象都经过点
和
两点；
②若该函数图象的对称轴为直线
，则必有
；
③当
时，
随
的增大而增大；
④若
，
是函数图象上的两点，如果
总成立，则
．
A.1个B.2个C.3个D.4个
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】下列说法正确的是（ ）
A.“打开电视机，正在播世界杯足球赛”是必然事件
B.甲组数据的方差是
，乙组数据的方差是
，则乙组数据比甲组数据稳定
C.一组数据2，3，4，5，5，6的众数和中位数都是5
D.“掷一枚硬币，正面朝上的概率是0.5”表示每抛掷硬币2次就有1次正面朝上
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】给定一个函数，如果这个函数的图象上存在一个点，它的横、纵坐标相等，那么这个点叫做该函数的不变点．
（1）一次函数
的不变点的坐标为______．
（2）二次函数
的两个不变点分别为点
（
在
的左侧），将点绕点顺时针旋转90°得到点
，求点的坐标．
（3）已知二次函数
的两个不变点的坐标为
．
①求
的值；
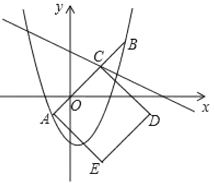
②如图，设抛物线与线段
围成的封闭图形记作
．点
为一次函数
的不变点，以线段
为边向下作正方形
．当
两点中只有一个点在封闭图形的内部（不包含边界）时，求出
的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：①abc＞0；②4a+2b+c＞0；③
＜a＜
；④b＞c．其中含所有正确结论的选项是（ ）
A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目：初中数学 来源： 题型：
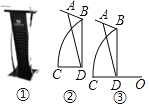
【题目】图①是一个演讲台，图②是演讲台的侧面示意图，支架BC是一段圆弧，台面与两支架的连接点A，B间的距离为30cm，CD为水平地面，∠ADC＝75°，∠DAB＝60°，BD⊥CD．
（1）求BD的长（结果保留整数，参考数据：sin75°≈0.97，cos75°≈0.26，
≈1.7）；
（2）如图③，若圆弧BC所在圆的圆心O在CD的延长线上，且OD＝CD，求支架BC的长（结果保留根号）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线
与
轴、
轴相交于
、
两点，抛物线
过点、，且与轴另一个交点为
，以
、
为边作矩形
，
交抛物线于点
．
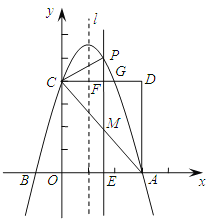
（1）求抛物线的解析式以及点的坐标；
（2）已知直线
交于点
，交于点
，交
于点
，交抛物线（上方部分）于点
，请用含
的代数式表示
的长；
（3）在（2）的条件下，连接
，若
和
相似，求的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
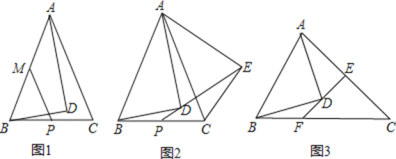
【题目】在
中，以
为斜边，作直角
，使点
落在内，
．
（1）如图1，若
，
，
，点，
、
分别为
，的中点，连接
，求线段的长；
（2）如图2，若，把绕点
递时针旋转一定角度，得到
，连接
并延长变于点，求证：
；
（3）如图3，若
，过点的直线交
于点
，交于点
，
，且
，请直接写出线段
、
、
之间的关系（不需要证明）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形
的对角线交于点
．点
在
边上，
连结
交对角线
于点
是线段
的中点，连结
．
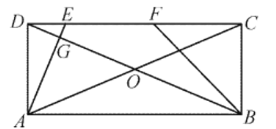
（1）求证：
．
（2）判断
与的数量关系，并说明理由．
（3）若
和
面积分别为
和
，求
的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
过点
．
（1）若点
也在该抛物线上，请用含
的关系式表示
；
（2）若该抛物线上任意不同两点
、
都满足：当
时，
；当
时，
；若以原点
为圆心，
为半径的圆与抛物线的另两个交点为
、
（点在点左侧），且
有一个内角为
，求抛物线的解析式；
（3）在（2）的条件下，若点
与点关于点
对称，且、
、
三点共线，求证：
平分
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
