
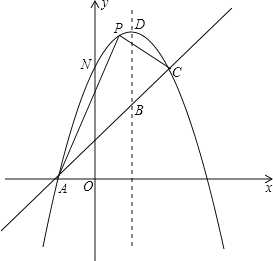
����Ŀ����ͼ����֪������y=��x2+bx+c��һֱ���ཻ��A(��1��0)��C(2��3)���㣬��y�ύ�ڵ�N���䶥��ΪD��
��1��������ֱ��AC�ĺ�����ϵʽ��
��2���������ߵĶԳ�����ֱ��AC�ཻ�ڵ�B��EΪֱ��AC�ϵ�����һ�㣬����E��EF��BD���������ڵ�F����B��D��E��FΪ������ı����ܷ�Ϊƽ���ı��Σ����ܣ����E�����ꣻ�����ܣ���˵�����ɣ�
��3����P����������λ��ֱ��AC�Ϸ���һ�����㣬���APC����������ֵ��
���𰸡���1��y=��x2+2x+3��y=x+1����2�����������ĵ�E������Ϊ(0��1)��(![]() ��
��![]() )��(
)��(![]() ��
��![]() )����3����������ֵΪ
)����3����������ֵΪ![]() ��
��
��������
��1�����ݵ�A��B�����꣬���ô���ϵ�����������������ֱ��AC�ĺ�����ϵʽ��
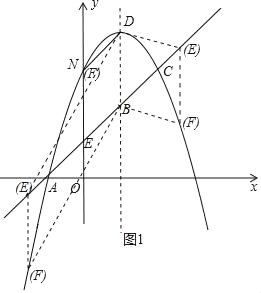
��2�������䷽����һ�κ���ͼ���ϵ�������������������B��D�����꣬���E������Ϊ��x��x+1�����ֵ�E���߶�AC�ϼ���E���߶�AC����CA���ӳ���������������ǣ�������E���߶�AC��ʱ����F�ڵ�E�Ϸ�����BD�ij���ϵ�E������ɵó���F������Ϊ��x��x+3���������ö��κ���ͼ���ϵ���������������x��ֵ�������ɵó���E�����ꣻ������E���߶�AC����CA���ӳ�����ʱ����F�ڵ�E�·�����BD�ij���ϵ�E������ɵó���F������Ϊ��x��x��1���������ö��κ���ͼ���ϵ���������������x��ֵ�������ɵó���E�����꣮���ϣ����ʵý⣻
��3������P��PM��x�ᣬ����Ϊ��M������C��CN��x�ᣬ����ΪN�����P������Ϊ��x����x2+2x+3������1��x��2�������M������Ϊ��x��0������ϵ�A��C�����꼰S��APC��S��APM+S����PMNC��S��ACN���ɵó�S��APC����x�ĺ�����ϵʽ�������ö��κ��������ʼ��ɽ����ֵ���⣮
�⣺��1����A����1��0����C��2��3������y����x2+bx+c���ã�
![]() ����ã�
����ã�![]() ��
��
�������ߵĺ�����ϵʽΪy����x2+2x+3��
��ֱ��AC�ĺ�����ϵʽΪy��kx+a��k��0����
��A����1��0����C��2��3������y��kx+a���ã�
![]() ����ã�
����ã�![]() ��
��
��ֱ��AC�ĺ�����ϵʽΪy��x+1��
��2����y����x2+2x+3������x��1��2+4��
���D��������1��4����
��x��1ʱ��y��x+1��2��
���B��������1��2����
���E��������x��x+1����
������������ǣ���ͼ1����
������E���߶�AC��ʱ����F�ڵ�E�Ϸ���
���F��������x��x+3����
�ߵ�F���������ϣ�
��x+3����x2+2x+3��
��ã�x1��0��x2��1����ȥ����
���E��������0��1����
������E���߶�AC����CA���ӳ�����ʱ����F�ڵ�E�·���
���F��������x��x��1����
�ߵ�F���������ϣ�
��x��1����x2+2x+3��
��ã�![]() ��
��
���E��������![]() ����
����![]() ��
��![]() ����
����
���ϣ����������ĵ�E������Ϊ��0��1������![]() ����
����![]() ��
��![]() ����
����
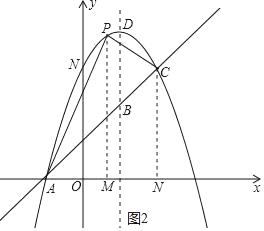
��3������P��PM��x�ᣬ����Ϊ��M������C��CN��x�ᣬ����ΪN����ͼ2��ʾ��
���P��������x����x2+2x+3������1��x��2�������M��������x��0����
�ߵ�A������Ϊ����1��0������C������Ϊ��2��3����
��AM��x+1��MN��2��x��PM����x2+2x+3��CN��3��AN��3��
��S��APC��S��APM+S����PMNC��S��ACN��
![]()
![]()
![]() ��
��
![]()
�൱x��![]() ʱ��S��APCȡ�����ֵ�����ֵΪ
ʱ��S��APCȡ�����ֵ�����ֵΪ![]() ����ʱ��P������Ϊ��
����ʱ��P������Ϊ��![]() ����
����


 ���������ν�ϵ�д�
���������ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
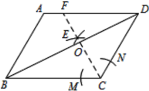
����Ŀ����ͼ����ƽ���ı���ABCD�У�AB=4��BC=5����ABC=60���� �����²�����ͼ������CΪԲ�ģ����ʵ���Ϊ�뾶��������CB��CD��M��N���㣻���ֱ���M��NΪԲ�ģ��Դ���![]() MN�ij�Ϊ�뾶�����������ཻ�ڵ�E��������CE��BD�ڵ�O����AD���ڵ�F����BO�ij���Ϊ��������
MN�ij�Ϊ�뾶�����������ཻ�ڵ�E��������CE��BD�ڵ�O����AD���ڵ�F����BO�ij���Ϊ��������
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y����2x+c��x���ڵ�A��3��0������y���ڵ�B��������y����x2+bx+c������A��B��
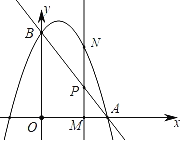
��1���������ߵĽ���ʽ��
��2����M��m��0�����߶�OA��һ���㣨��M�����O��A�غϣ�������M��y���ƽ���ߣ���ֱ��AB�ڵ�P�����������ڵ�N����NP��![]() AP����m��ֵ��
AP����m��ֵ��
��3�����������ϴ��ڵ�Q��ʹ��QBA��45������ֱ��д����Ӧ�ĵ�Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ں�����ѧϰ�У����Ǿ�������ȷ����������ʽ��������ͼ�����ú���ͼ���о��������ʩ�����ͼ������������ѧϰ���̣��ڻ�����ͼ��ʱ�����dz���ͨ������ƽ�ƻ��۵ķ���������ͼ��С������ѧ���ĺ���֪ʶ̽������y1�� ��ͼ�������ʲ�����ͼ�������⣮С���г������y1��x�ļ����Ӧ��ֵ��
��ͼ�������ʲ�����ͼ�������⣮С���г������y1��x�ļ����Ӧ��ֵ��
x | �� | ��4 | ��3 | ��2 | ��1 | 0 | 1 | 2 | 3 | 4 | �� |
y1 | �� | 4 | 2 | m | 2 | 4 | 2 |
| n |
| �� |
��1�����ݱ�����x��y1�Ķ�Ӧ��ϵ�ɵ�m��______��n��______��
��2����ƽ��ֱ������ϵ�У���������и��㣬�����ú���ͼ���ݺ���ͼ��д���ú�����һ������______��
��3��������y1��ͼ����ֱ��y2��mx+1����������ʱ��ֱ��д��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
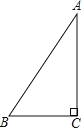
����Ŀ����ͼ����֪Rt��ABC�С�C=90�㣬AB=10��AC=8��
��1����AB�Ĵ�ֱƽ����DE����AB�ڵ�D����AC�ڵ�E��(Ҫ��߹���ͼ����д������������ͼ�ۼ�)��
��2����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ӿ����Խӣ�����ȫ��������壬ij������A��B���ؼ�Ĺ�·���иĽ�����ͼ��A��B����֮����һ��ɽ������ԭ����A�ص�B����;��C��������ACB��ʻ���ֿ�ͨ������������ֱ����ֱ��AB��ʻ����֪BC=80ǧ�ף���A=45�㣬��B=30�㣮
��1����ͨ����ǰ��������A�ص�B�ش�ԼҪ�߶���ǧ�ף�
��2����ͨ������������A�ص�B�ش�Լ�������߶���ǧ�ף��������ȷ��0.1ǧ�ף����ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ1����ƽ���ı���ABCD�У���E1��E2��AB���ȷֵ㣬��F1��F2��CD���ȷֵ㣬E1F1��E2F2�ֱ�AC�ڵ�G1��G2����֤��AG1��G1G2��G2C��
(2)��ͼ2����64���߳�Ϊ1��С��������ɵ�һ������ͼ���߶�MN�������˵��ڸ���ϣ�����һ���̶ȵij��ӣ������߶�MN���ȷֵ�P��Q��(������ͼ�ۼ�)
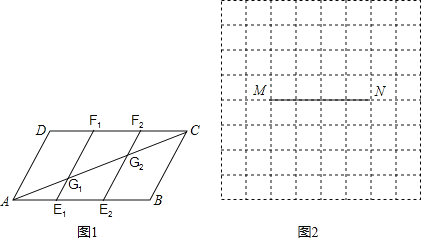
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������(����)��
A.�ҵĴ�ֱƽ���߱�ƽ�������Ե���������
B.��һö���ȵ����ӣ�����ֹͣת����2�㳯��������¼���
C.��Rt��ABC�����߳�ǡΪ����x2-7x+12=0������ʵ����������б�߳�Ϊ5��
D.��ֱ��y=ax-b��ֱ��y=mx+n���ڵ�(2��-1)����![]() �Ľ�Ϊ
�Ľ�Ϊ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊ
Ϊ![]() ��һ�㣬������
��һ�㣬������![]() ��
��![]() ��
��![]() �ֱ�
�ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ������
������![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
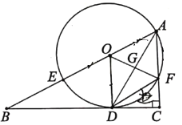
��1����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2����![]() ��
��![]() �����ú�
�����ú�![]() ��
��![]() �Ĵ���ʽ��ʾ�߶�
�Ĵ���ʽ��ʾ�߶�![]() �ij���
�ij���
��3����![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com