

分析 [问题探究]:
(3)如图4,把长、宽、高三边的线段条数相乘即可求解;
(4)先得到宽共有多少条线段,高共有多少条线段,再把长、宽、高三边的线段条数相乘即可求解;
(5)先根据数线段的方法得到长、宽、高三边的线段条数,再把它们相乘即可求解;
[结论应用]
(6)由(5)的结论,根据等量关系:由若干个小立方块组成的正方体中共有1000个长方体,列出方程求解即可.
解答 解:[问题探究]:
(3)3×3×3=27(个).
答:图中共有27个长方体.
(4)4×3÷2=6(条),
7×6÷2=21(条),
3×6×21=378(个).
答:宽共有6条线段,高共有21条线段,图中共有63个长方体.
(5)长、宽、高各有$\frac{n(n+1)}{2}$线段,所以图中共有[$\frac{n(n+1)}{2}$]3=$\frac{{n}^{3}(n+1)^{3}}{8}$个长方体.
[结论应用]
(6)依题意有:
[$\frac{n(n+1)}{2}$]3=1000,
$\frac{n(n+1)}{2}$=10,
解得n1=4,n2=-5(不合题意舍去),
4×4×4=64(个).
答:组成这个正方体的小立方块的个数是64个.
故答案为:27;6,21,63;$\frac{n(n+1)}{2}$,$\frac{{n}^{3}(n+1)^{3}}{8}$.
点评 考查了立体图形,组合图形中线段的计数,本题关键是得到n×n×n个小立方块组成的正方体中共有[$\frac{n(n+1)}{2}$]3个长方体.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
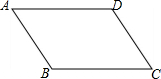 如图,已知四边形ABCD是平行四边形,AB<AD.
如图,已知四边形ABCD是平行四边形,AB<AD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 | 第八次 | 第九次 | 第十次 | 第十一次 |
| +15 | -2 | +5 | -1 | +10 | -3 | -2 | +12 | +4 | -5 | +6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
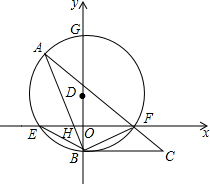 如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在⊙D上,连接AB交x轴于点H,连接AF并延长到点C,使∠FBC=∠A.
如图,在平面直角坐标中,点D在y轴上,以D为圆心,作⊙D交x轴于点E、F,交y轴于点B、G,点A在⊙D上,连接AB交x轴于点H,连接AF并延长到点C,使∠FBC=∠A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com