
【题目】如图,直线![]() 与x轴、y轴分别交于C、D两点,与双曲线
与x轴、y轴分别交于C、D两点,与双曲线![]() 在第一象限内交于点P,过点P作
在第一象限内交于点P,过点P作![]() 轴于点A,
轴于点A,![]() 轴于点B,已知
轴于点B,已知![]() 且
且![]()
![]() 直接写出直线的解析式______,双曲线的解析式______;
直接写出直线的解析式______,双曲线的解析式______;
![]() 设点Q是直线
设点Q是直线![]() 上的一点,且满足
上的一点,且满足![]() 的面积是
的面积是![]() 面积的2倍,请求出点Q的坐标.
面积的2倍,请求出点Q的坐标.

科目:初中数学 来源: 题型:
【题目】已知:平面直角坐标系中,把点A(m,4)(m是实数)向右移动7个单位向下移动2个单位得到点B,点B向左移动3个单位向上移动6个单位得到点C,请解答:
(1) 点B,C的坐标是:B ,C ;
(2) 求△ABC的面积;
(3)若连接OC交线段AB于点D,且△ACD与△BCD的面积比不超过0.75时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
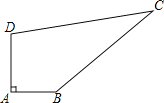
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B. 甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
C. “明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D. 了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法①△BDF≌△CDE;②△ABD和△ACD面积相等;③BF∥CE;④CE=BF.其中正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次质检抽测中,随机抽取某摊位20袋食盐,测得各袋的质量分别为(单位:g):492,496,494,495,498,497,501,502,504,496,497,503,506,508,507,492,496,500,501,499,根据以上抽测结果,任买一袋该摊位的食盐,质量在497.5 g~501.5 g之间的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一项资助贫困生的公益活动由你来主持,每位参与者需交赞助费5元,活动规则如下:如图是两个可以自由转动的转盘,每个转盘被分成6个相等的扇形,参与者转动这两个转盘,转盘停止后,指针各自指向一个数字,(若指针在分格线上,则重转一次,直到指针指向某一数字为止),若指针最后所指的数字之和为12,则获得一等奖,奖金20元;数字之和为9,则获得二等奖,奖金10元;数字之和为7,则获得三等奖,奖金为5元;其余均不得奖;此次活动所集到的赞助费除支付获奖人员的奖金外,其余全部用于资助贫困生的学习和生活;
(1)分别求出此次活动中获得一等奖、二等奖、三等奖的概率;
(2)若此次活动有2000人参加,活动结束后至少有多少赞助费用于资助贫困生?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小章为学校举办的数学文化节没计的标志,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空自部分面积为10.5,则阴影部分面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】著名的恩施大峡谷(A)和世界级自然保护区星斗山(B)位于笔直的沪渝高速公路X同侧,AB=50km,A、B到直线X的距离分别为10km和40km,要在沪渝高速公路旁修建一服务区P,向A、B两景区运送游客.小民设计了两种方案,图1是方案一的示意图(AP与直线X垂直,垂足为P),P到A、B的距离之和S1=PA+PB,图2是方案二的示意图(点A关于直线X的对称点是A',连接BA′交直线X于点P),P到A、B的距离之和S2=PA+PB

(1)S1=_____km.S2=_____km.
(2)PA+PB的最小值为_____km.
(3)拟建的恩施到张家界高速公路与沪渝高速公路垂直,建立如图3所示的直角坐标系,B到直线的距为30km,请你在X旁和P旁各修建一服务区P、Q,使P、A、B、Q组成的四边形的周长最小,(用尺画出点P和点Q的位置)这个最小值为_____km.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com