
分析 先把代数式按照多项式乘以多项式展开,因为化简后是一个四次多项式,所以x的最高指数m+2=4;不含二次项,即二次项的系数为0,即可解答.
解答 解:(mx2+2mx-1)(xm+3nx+2)=mxm+2+3mnx3+2mx2+2mxm+1+6mnx2+4mx-xm-3nx-2,
因为该多项式是四次多项式,
所以m+2=4,
解得:m=2,
原式=2x4+(6n+4)x3+(3+12n)x2+(8-3n)x-2
∵多项式不含二次项
∴3+12n=0,
解得:n=$-\frac{1}{4}$,
所以一次项系数8-3n=8.75.
点评 本题考查了多项式乘以多项式,解决本题的关键是明确化简后是一个四次多项式,所以x的最高指数m+2=4;不含二次项,即二次项的系数为0,即可解答.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
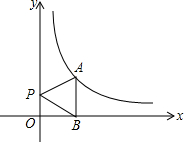 已知点A(m、n)是反比例函数$y=\frac{4}{x}$(x>0)的图象上一点,过A作AB⊥x轴于点B,P是y轴上一点,
已知点A(m、n)是反比例函数$y=\frac{4}{x}$(x>0)的图象上一点,过A作AB⊥x轴于点B,P是y轴上一点,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线相互平分的四边形是平行四边形 | |
| B. | 对角线相互平分且相等的四边形是矩形 | |
| C. | 对角线相互平分且垂直的四边形是菱形 | |
| D. | 对角线相等且垂直的四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{5}}}{2}$ | B. | $3\sqrt{5}$ | C. | $\frac{{6\sqrt{5}}}{5}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com