
����Ŀ����ƽ��ֱ������ϵ�У���֪������y��![]() x2+bx+c��ͼ����x�ύ�ڵ�A����2��0������B��6��0������y�ύ�ڵ�C������ΪD��
x2+bx+c��ͼ����x�ύ�ڵ�A����2��0������B��6��0������y�ύ�ڵ�C������ΪD��
��1���������ߵĽ���ʽ��
��2����E���߶�AB�ϵĵ㣬ֱ��EM��x�ᣬ���E�ĺ�����Ϊt��
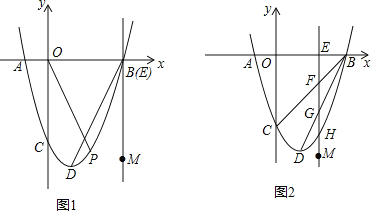
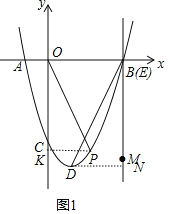
�ٵ�t��6ʱ����ͼ1������PΪx���·��������ϵ�һ�㣬����COP����DBM�����ʱ��P�ĺ����ꣻ
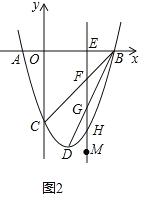
�ڵ�2��t��6ʱ����ͼ2����ֱ��EM���߶�BC��BD�������߷ֱ��ཻ�ڵ�F��G��H����֤���߶�EF��FG��GH������ɵ��������Σ�����˵��������εǵ�����ֵΪ![]() ����˵��������ε������
����˵��������ε������
���𰸡�(1) y��![]() x2��2x��6��(2)�ٵ�P�ĺ�����Ϊ2
x2��2x��6��(2)�ٵ�P�ĺ�����Ϊ2![]() ����
����![]() ��
��
��������
��1������������y��![]() x2+bx+c��ͼ����x�ύ��A����2��0����B��6��0�������ý���ʽ��ȷ�������߽���ʽ��
x2+bx+c��ͼ����x�ύ��A����2��0����B��6��0�������ý���ʽ��ȷ�������߽���ʽ��
��2���ٹ���D��DN��BM��N������P��PK��y����K������tan��DBN���ٸ��������COP=��DBM����tan��COP=tan��DBN�������P�ĺ����ꣻ
�ڴ���ϵ������ã�ֱ��BC�Ľ���ʽΪy=x-6��ֱ��BD�Ľ���ʽΪy=2x-12����ʾ��F��G��H�����꣬����֤�����߶�EF��FG��GH������ɵ��������Σ��ټ������߶�EF��FG��GH��ɵ��������ε������
�⣺��1������������y��![]() x2+bx+c��ͼ����x�ύ��A����2��0����B��6��0����
x2+bx+c��ͼ����x�ύ��A����2��0����B��6��0����
�������߽���ʽΪy��![]() ��x+2����x��6����
��x+2����x��6����
��y��![]() x2��2x��6��
x2��2x��6��
��2������ͼ1������D��DN��BM��N������P��PK��y����K��
���BND����OCP��90��
��y��![]() ��x��2��2��8
��x��2��2��8
��D��2����8����B��6��0����N��6����8����
��tan��DBN��![]() ��
��![]() ��
��![]() ��
��
�ߡ�COP����DBM��
��tan��COP��tan��DBN��![]() ��
��
��P��m��![]() ��2m��6������KP��m��OK������
��2m��6������KP��m��OK������![]() ��2m��6��
��2m��6��
��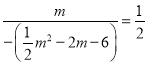 ����ã�m1����2
����ã�m1����2![]() �����������⣬��ȥ����m2��2
�����������⣬��ȥ����m2��2![]() ��
��
���P�ĺ�����Ϊ2![]() ��
��
����ͼ2����B��6��0����C��0����6����D��2����8����
��ֱ��BC�Ľ���ʽΪy��x��6��ֱ��BD�Ľ���ʽΪy��2x��12��
��E��t��0����
��F��t��t��6����G��t��2t��12����H��t��![]() ��2t��6��
��2t��6��
��EF��6��t��FG��t��6����2t��12����6��t��GH��2t��12����![]() ��2t��6������
��2t��6������![]() +4t��6��
+4t��6��
��EF��FG
��EF+FG��12��2t��EF+FG��GH��12��2t������![]() +4t��6����
+4t��6����![]() ��6t+18��
��6t+18��![]() ��
��
�൱2��t��6ʱ��![]() ��0����EF+FG��GH
��0����EF+FG��GH
���߶�EF��FG��GH������ɵ��������Σ�
��ͼ3����RTS�У���RT��RS��6��t��TS����![]() +4t��6����RL��TS��L�����RLT��90��
+4t��6����RL��TS��L�����RLT��90��
��RT��RS��RL��TS
��TL��![]() TS����
TS����![]() +2t��3
+2t��3
��������cos��RTS��![]() ����
����![]() ��
��![]()
��2��6��t����3����![]() +2t��3������ã�t1��6�����������⣬��ȥ����t2��
+2t��3������ã�t1��6�����������⣬��ȥ����t2��![]() ��
��
��TL��![]() ��TS��
��TS��![]() ��RT��
��RT��![]()
��RL��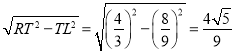
��S��RTS��![]() TSRL��
TSRL��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
���߶�EF��FG��GH��ɵĵ��������ε����Ϊ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��Խ���AC��BD����O�㣬DE��AC��CE��BD��
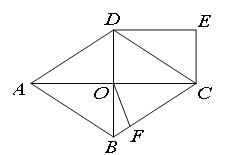
��1����֤���ı���OCEDΪ���Σ�
��2����BC�Ͻ�ȡCF��CO������OF����AC��16��BD��12�����ı���OFCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������B����2��0����ֱ��y��kx+b��ֱ��y��4x+2�ཻ�ڵ�A����1����2����4x+2��kx+b��0�Ľ⼯Ϊ��������
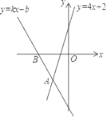
A.x����2B.��2��x����1C.x����1D.x����1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
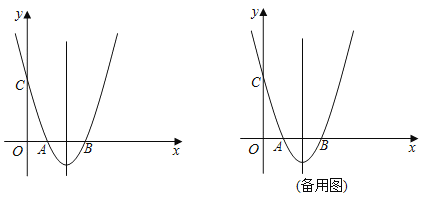
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y��x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C���Գ���Ϊֱ��x��2����A������Ϊ��1��0����
��1����������ߵı���ʽ���������ꣻ
��2����PΪ��������һ�㣨�����A�غϣ�������PC������PCB����ACBʱ�����P�����ꣻ
��3���ڣ�2���������£�����������ƽ����y��ķ�������ƽ�ƣ�ƽ�ƺ�������ߵĶ���Ϊ��D����P�Ķ�Ӧ��Ϊ��Q����OD��DQʱ����������ƽ�Ƶľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У���BAD��120�㣬��B����D��90������BC��CD�Ϸֱ���һ��M��N��ʹ��AMN�ܳ���Сʱ�����AMN����ANM�Ķ�����________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ������
��ֱ������![]() ��
��![]() �ϣ���
�ϣ���![]() �ǻ�
�ǻ�![]() ���е㣬
���е㣬![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() �ӳ�����һ�㣬����
�ӳ�����һ�㣬����![]() ����
����![]() ��
��

��1�����ж�ֱ��![]() ��
��![]() ��λ�ù�ϵ����˵�����ɣ�
��λ�ù�ϵ����˵�����ɣ�
��2����![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
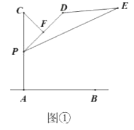
����Ŀ�������ȵ��ļ�������ɡ�����ǵ��������洦�ɼ�����ͼ�٣���������ʽ����ɡ������![]() ֱ�ڵ���
ֱ�ڵ���![]() ����
����![]() Ϊ�����ϵĻ������ڵ㣬ɡ��Ľ���ʾ��ͼΪ
Ϊ�����ϵĻ������ڵ㣬ɡ��Ľ���ʾ��ͼΪ![]() ��
��![]() Ϊ
Ϊ![]() �е㣬
�е㣬![]() ��
��![]() ��
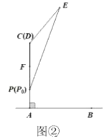
��![]() ������
������![]() λ�ڳ�ʼλ��
λ�ڳ�ʼλ��![]() ʱ����
ʱ����![]() ��
��![]() �غϣ���ͼ�ڣ�����������飬��̫��������
�غϣ���ͼ�ڣ�����������飬��̫��������![]() ��ֱʱ������Ч����ѣ���֪̫�����������ļн�Ϊ
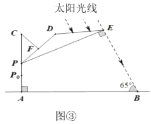
��ֱʱ������Ч����ѣ���֪̫�����������ļн�Ϊ![]() ����ͼ�ۣ���Ϊʹ����Ч����ѣ���
����ͼ�ۣ���Ϊʹ����Ч����ѣ���![]() ���
���![]() �ϵ������ף��������ȷ��
�ϵ������ף��������ȷ��![]() �����ο����ݣ�
�����ο����ݣ�![]() ��
��![]() ��
��![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����E��F�ֱ���AB��BC�ϣ���AE=BF=1��CE��DF���ڵ�O�����н��ۣ��١�DOC=90�㣬��OC=OE����CE=DF����tan��OCD=![]() ����S��DOC=S�ı���EOFB�У���ȷ���У�������
����S��DOC=S�ı���EOFB�У���ȷ���У�������
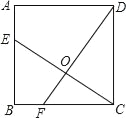
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ҹ��������ķ�չ��������������������Խ��Խ�ߣ�ij����Ϊ���˽��ͥ�����Ļ������������Ŀ��������ȡ���ּ�ͥ����ÿ����ͥ���Ļ����������ѽ������ʾ����ˣ����ݵ��������Ƴ�������������ͳ��ͼ����
�������ͳ��ͼ���ṩ����Ϣ������������⣺
��e | ��ͥ���Ļ��������ѽ��x��Ԫ�� | ���� |
A | x��5000 | 36 |
B | 5000��x��10000 | m |
C | 10000��x��15000 | 27 |
D | 15000��x��20000 | 15 |
E | x��20000 | 30 |
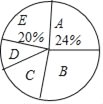
��1�����α����˵ļ�ͥ��__________�������� m=__________��
��2�����ε������ݵ���λ��������__________�飮����ͳ��ͼ�У�D���������ε�Բ�Ľ���__________�ȣ�
��3�����������2500����ͥ��������Ƽ�ͥ���Ļ���������10000Ԫ���ϵļ�ͥ�ж��ٻ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com