
分析 (1)根据完全平方公式把原式化为(x-4)2+(y+5)2=0的形式,根据非负数的性质求出x、y,代入代数式根据乘方法则计算即可;
(2)根据完全平方公式把原式化为(a-b)2+(b-c)2+(c-a)2=0的形式,根据非负数的性质进行解答即可.
解答 解:(1)∵x2+y2-8x+10y+41=0,
∴x2-8x+16+y2+10y+25=0.
∴(x-4)2+(y+5)2=0.
∴x-4=0且y+5=0.
∴x=4,y=-5.
∴(x+y)2016=[4+(-5)]2016=1.
(2)∵a2+b2+c2=ab+bc+ca,
∴2a2+2b2+2c2=2ab+2bc+2ca.
∴a2-2ab+b2+b2-2bc+c2+c2-2ca+a2=0.
∴(a-b)2+(b-c)2+(c-a)2=0.
∴a-b=0且b-c=0且c-a=0.
∴a=b=c.
∴△ABC是等边三角形.
点评 本题考查的是配方法的应用和非负数的性质的应用,正确根据完全平方公式进行配方是解题的关键.


科目:初中数学 来源: 题型:解答题
 5个棱长为1的正方体组成如图的几何体.
5个棱长为1的正方体组成如图的几何体.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点E是四边形ABCD的对角线BD上的一点,∠BAE=∠CBD=∠DAC.
如图,点E是四边形ABCD的对角线BD上的一点,∠BAE=∠CBD=∠DAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
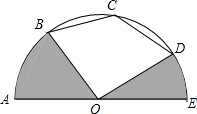 如图,半圆O的直径AE=4,点B、C、D均在半圆上,若AB=BC,CD=DE,连接OB、OD,
如图,半圆O的直径AE=4,点B、C、D均在半圆上,若AB=BC,CD=DE,连接OB、OD,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com