
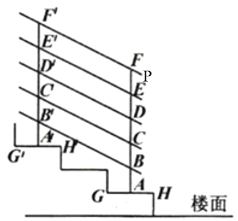
【题目】如图是楼梯一部分示意图,楼梯台阶宽度均为![]() ,高度均为
,高度均为![]() ,且
,且![]() ,
,![]() 均与楼面垂直,点
均与楼面垂直,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
(1)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求![]() 的值;
的值;
(3)求点![]() 到水平楼面的距离(精确到
到水平楼面的距离(精确到![]() ).
).
【答案】(1)![]() ∥
∥![]() ,理由见解析;(2)2;(3)
,理由见解析;(2)2;(3)![]()
【解析】
(1)由![]() 与FB平行且相等,得出四边形
与FB平行且相等,得出四边形![]() 是平行四边形,进而得出
是平行四边形,进而得出![]() ∥
∥![]() ;
;
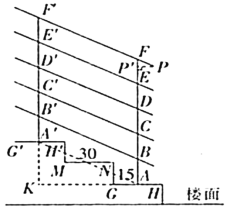
(2)延长![]() 、
、![]() 交于点K,连接
交于点K,连接![]() ,在Rt△
,在Rt△![]() 中,求出tan∠
中,求出tan∠![]() ,根据平行线的性质得出∠EFP=∠
,根据平行线的性质得出∠EFP=∠![]() ,由此得解;
,由此得解;
(3)过点P作![]() ,交AF于点
,交AF于点![]() ,根据
,根据![]() 的值得出
的值得出![]() 与
与![]() 的数量关系,在Rt△
的数量关系,在Rt△![]() 中,运用勾股定理求出
中,运用勾股定理求出![]() ,进而求出
,进而求出![]() 到水平楼面的距离.
到水平楼面的距离.
(1)![]() ∥
∥![]() ,理由:
,理由:
∵![]() ,
,![]() 均与楼面垂直
均与楼面垂直
∴![]() ∥
∥![]()
又∵![]()
![]()
∴![]() =
=![]()
∴四边形![]() 是平行四边形
是平行四边形
∴![]() ∥
∥![]() ;
;
(2)如图,延长![]() ,
,![]() 交于点K,连接
交于点K,连接![]() ,
,
∵![]() ,
,![]() 均与楼面垂直,
均与楼面垂直,
∴△![]() 是直角三角形,
是直角三角形,
∵楼梯台阶宽度均为![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴KA=![]()
∵楼梯高度均为![]() ,
,
∴![]()
在Rt△![]() 中,tan∠
中,tan∠![]() =
=![]()
∵![]() ∥
∥![]() ,
,
∴∠EFP=∠![]()
易证![]()
∴∠![]() =∠
=∠![]()
∴tan∠EFP=tan∠![]() =2;
=2;
(3)过点P作![]() ,交AF于点
,交AF于点![]() ,
,
在Rt△![]() 中,tan∠EFP=2
中,tan∠EFP=2
∴![]()
根据勾股定理,![]() ,即
,即![]()
∴![]() cm
cm
∴P到水平楼面的距离为16×5+15-![]() =95-
=95-![]() ≈91.4cm.
≈91.4cm.


科目:初中数学 来源: 题型:
【题目】小方与小辉在玩军棋游戏,他们定义了一种新的规则,用军棋中的“工兵”、“连长”、“地雷”比较大小,共有6个棋子,分别为1个“工兵”,2个“连长”,3个“地雷”游戏规则如下:①游戏时,将棋反面朝上,两人随机各摸一个棋子进行比赛,先摸者摸出的棋不放回;②“工兵”胜“地雷”,“地雷”胜“连长”,“连长”胜“工兵”;③相同棋子不分胜负.
(1)若小方先摸,则小方摸到“排长”的事件是 ;若小方先摸到了“连长”,小辉在剩余的5个棋子中随机摸一个,则这一轮中小方胜小辉的概率为 .
(2)如果先拿走一个“连长”,在剩余的5个棋子中小方先摸一个棋子,然后小辉在剩余的4个棋子中随机摸一个,求这一轮中小方获胜的概率 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
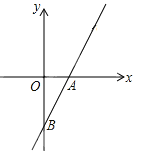
(1)求直线AB的解析式;
(2)直线AB上是否存在点C,使△BOC的面积为2?若存在,求出点C的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个分别标有数1,2,3,4的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为x,小颖在剩下的3个球中随机摸出一个小球记下数为y,这样确定了点P(x,y),请用“列表法”或“树状图法”求点P(x,y)在函数y=-x+5图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
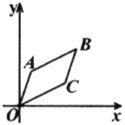
【题目】如图,已知![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() ,若将
,若将![]() 先沿
先沿![]() 轴进行第一次对称变换,所得图形沿
轴进行第一次对称变换,所得图形沿![]() 轴进行第二次对称变换,轴对称变换的对称轴遵循
轴进行第二次对称变换,轴对称变换的对称轴遵循![]() 轴、
轴、![]() 轴、
轴、![]() 轴、
轴、![]() 轴…的规律进行,则经过第2018次变换后,
轴…的规律进行,则经过第2018次变换后,![]() 顶点
顶点![]() 坐标为()
坐标为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年底,2020年初我国爆发了新冠肺炎疫情,为了增加学生对疫情和肺炎的预防知识的了解,某学校利用网络开展了相关知识的宣传教育活动,为了解这次的宣传效果,学校从全校3600名学生中随机抽取200名学生进行知识测试(满分100分,得分均为整数),并根据这200人的测试成绩,制订如下统计图表:

(1) ![]() ,
,![]() ,成绩最好的等级A所占的百分比;
,成绩最好的等级A所占的百分比;
(2)张亮在这次测试中成绩为85分,你认为85分一定是这200名学生知识测试成绩的中位数吗?请简要说明理由;
(3)如果80分以上(包括80分)为优秀,请估计全校3600名学生中成绩优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是反比例函数![]() 的图象,点
的图象,点![]() ,
,![]() 分别在图象的两支上,以
分别在图象的两支上,以![]() 为对角线作矩形
为对角线作矩形![]() 且
且![]() 轴.
轴.
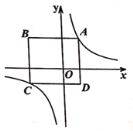
(1)当线段![]() 过原点时,分别写出
过原点时,分别写出![]() 与
与![]() ,
,![]() 与
与![]() 的一个等量关系式;
的一个等量关系式;
(2)当![]() 、
、![]() 两点在直线
两点在直线![]() 上时,求矩形
上时,求矩形![]() 的周长;
的周长;
(3)当![]() 时,探究
时,探究![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=4![]() ,∠C=90°,点D在BC上,且CD=3DB,将△ABC折叠,使点A与点D重合,EF为折痕,则tan∠BED的值是_____.
,∠C=90°,点D在BC上,且CD=3DB,将△ABC折叠,使点A与点D重合,EF为折痕,则tan∠BED的值是_____.
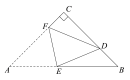
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图1,图2分别是某款高压电塔的实物图和示意图电塔的底座AB与地面平齐,DF表示电塔顶端D到地面的距离,已知AF的长是2米,支架AC与地面夹角∠BAC=86°,顶端支架DC长10米,DC与水平线CE之间夹角∠DCE=45°,求电塔的高度DF.(sin86°=0.998,cos86°=0.070,tan86°=14.300,![]() ≈1.4,结果保留整数)
≈1.4,结果保留整数)
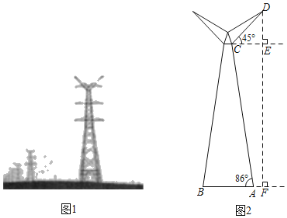
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com