
ЁОЬтФПЁПдФЖСЯТУцВФ
гавРДЮХХСаЕФ![]() ИіЪ§ЃК
ИіЪ§ЃК![]() ЖдШЮвтЯрСкЕФСНИіЪ§ЃЌЖМгУгвБпЕФЪ§МѕШЅзѓБпЕФЪ§ЃЌЫљЕУжЎВюаДдкетСНИіЪ§жЎМфЃЌПЩВњЩњвЛИіаТЪ§ДЎЃК
ЖдШЮвтЯрСкЕФСНИіЪ§ЃЌЖМгУгвБпЕФЪ§МѕШЅзѓБпЕФЪ§ЃЌЫљЕУжЎВюаДдкетСНИіЪ§жЎМфЃЌПЩВњЩњвЛИіаТЪ§ДЎЃК ![]() етГЦЮЊЕквЛДЮВйзїЃЛЕкЖўДЮЭЌбљЕФВйзїКѓвВПЩВњЩњвЛИіаТЪ§ДЎЃК
етГЦЮЊЕквЛДЮВйзїЃЛЕкЖўДЮЭЌбљЕФВйзїКѓвВПЩВњЩњвЛИіаТЪ§ДЎЃК![]() МЬајвРДЮВйзїЯТШЅЃЎЮЪ
МЬајвРДЮВйзїЯТШЅЃЎЮЪ
![]() гавРДЮХХПЊЕФ
гавРДЮХХПЊЕФ![]() ИіЪ§ЃК
ИіЪ§ЃК ![]() ЃЌЕквЛДЮВйзїКѓЃЌдіМгЕФЫљгааТЪ§жЎКЭЪЧЖрЩй?
ЃЌЕквЛДЮВйзїКѓЃЌдіМгЕФЫљгааТЪ§жЎКЭЪЧЖрЩй?
![]() дк
дк![]() ЕФЧАЬсЯТЃЌОЙ§ЕкЖўДЮВйзїКѓЫљЕУЕФаТЪ§ДЎБШЕквЛДЮВйзїКѓЫљЕУЕФЪ§ДЎдіМгЕФЫљгааТЪ§жЎКЭЪЧЖрЩй?
ЕФЧАЬсЯТЃЌОЙ§ЕкЖўДЮВйзїКѓЫљЕУЕФаТЪ§ДЎБШЕквЛДЮВйзїКѓЫљЕУЕФЪ§ДЎдіМгЕФЫљгааТЪ§жЎКЭЪЧЖрЩй?
![]() ВТЯыЃКгавРДЮХХПЊЕФ
ВТЯыЃКгавРДЮХХПЊЕФ![]() ИіЪ§ЃЌ
ИіЪ§ЃЌ![]() ЕквЛАйДЮВйзїКѓЕУЕНЕФаТЪ§ДЎБШЕкОХЪЎОХДЮВйзїКѓЫљЕУЕФЪ§ДЎдіМгЕФЫљгааТЪ§жЎКЭЪЧЖрЩй?
ЕквЛАйДЮВйзїКѓЕУЕНЕФаТЪ§ДЎБШЕкОХЪЎОХДЮВйзїКѓЫљЕУЕФЪ§ДЎдіМгЕФЫљгааТЪ§жЎКЭЪЧЖрЩй?
ЁОД№АИЁПЃЈ1ЃЉ4ЃЛЃЈ2ЃЉ4ЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉЗТдьЬтвтЫљИјЕФЕквЛДЮВйзїЕФФЃЪННЋДЫЪБЕФШ§ИіЪ§МгвдВйзїМДПЩЃЛ
ЃЈ2ЃЉИљОнЃЈ1ЃЉПЩжЊЕквЛДЮВйзїКѓЕФаТЪ§ДЎЮЊЃК![]() ЃЌОнДЫНјвЛВННјааЕкЖўДЮВйзїМДПЩЕУГіЕкЖўДЮВйзїКѓЕФаТЪ§ДЎЃЌШЛКѓНјвЛВНМЦЫуМДПЩЃЛ
ЃЌОнДЫНјвЛВННјааЕкЖўДЮВйзїМДПЩЕУГіЕкЖўДЮВйзїКѓЕФаТЪ§ДЎЃЌШЛКѓНјвЛВНМЦЫуМДПЩЃЛ
ЃЈ3ЃЉЪзЯШЧѓГіИУзщЪ§ЕквЛДЮВйзїКѓЫљЕУЕФаТЪ§ДЎЕФдіМгЕФаТЪ§жЎКЭЃЌШЛКѓИљОнЃЈ1ЃЉЁЂЃЈ2ЃЉжаЕФНсЙћЗЂЯжЦфЧАКѓЕквЛЁЂЕкЖўЯрСкСНДЮЕФВйзїКѓЫљЕУЕФаТЪ§ДЎЕФдіМгЕФаТЪ§жЎКЭВЂУЛгаЗЂЩњБфЛЏЃЌОнДЫНјвЛВНВТЯыМДПЩ.
ЃЈ1ЃЉгЩЬтвтЕУПЩЕУЃК
НЋ![]() ЕквЛДЮВйзїКѓЫљЕУЕФаТЪ§ДЎЮЊЃК
ЕквЛДЮВйзїКѓЫљЕУЕФаТЪ§ДЎЮЊЃК![]() ЃЌ
ЃЌ
ЦфжадіМгЕФаТЪ§ЮЊЃК![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МДЕквЛДЮВйзїКѓЃЌдіМгЕФЫљгааТЪ§жЎКЭЪЧ4ЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩЕУЕквЛДЮВйзїКѓЕФаТЪ§ДЎЮЊЃК![]() ЃЌ
ЃЌ
ЁрЕкЖўДЮВйзїКѓЕФаТЪ§ДЎЮЊЃК![]() ЃЌ
ЃЌ
ЦфжадіМгЕФаТЪ§ЮЊЃК![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МДЕкЖўДЮВйзїКѓЫљЕУЕФаТЪ§ДЎБШЕквЛДЮВйзїКѓЫљЕУЕФЪ§ДЎдіМгЕФЫљгааТЪ§жЎКЭЮЊ4ЃЛ
ЃЈ3ЃЉгЩЬтвтЕУЃК![]() ЕквЛДЮВйзїКѓПЩЕУаТЪ§ДЎЮЊЃК
ЕквЛДЮВйзїКѓПЩЕУаТЪ§ДЎЮЊЃК![]() ЃЌ
ЃЌ
ДЫЪБаТдіМгЕФЪ§ЮЊЃК![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МДЕкЖўДЮВйзїКѓЫљЕУЕФаТЪ§ДЎБШЕквЛДЮВйзїКѓЫљЕУЕФЪ§ДЎдіМгЕФЫљгааТЪ§жЎКЭЮЊ![]() ЃЌ
ЃЌ
ИљОнЃЈ1ЃЉЁЂЃЈ2ЃЉЕФД№АИПЩвдЗЂЯжЃЌЦфЧАКѓЕквЛЁЂЕкЖўДЮЕФВйзїКѓЫљЕУЕФаТЪ§ДЎЕФдіМгЕФаТЪ§жЎКЭВЂУЛгаЗЂЩњБфЛЏЃЌ
Ёр ВТЯыЗВЪЧЧАКѓСНДЮЯрСкВйзїКѓЫљЕУЕФаТЪ§ДЎЕФдіМгЕФаТЪ§жЎКЭВЛЛсЗЂЩњБфЛЏЃЌ
Ёр![]() ЕквЛАйДЮВйзїКѓЕУЕНЕФаТЪ§ДЎБШЕкОХЪЎОХДЮВйзїКѓЫљЕУЕФЪ§ДЎдіМгЕФЫљгааТЪ§жЎКЭЮЊЃК
ЕквЛАйДЮВйзїКѓЕУЕНЕФаТЪ§ДЎБШЕкОХЪЎОХДЮВйзїКѓЫљЕУЕФЪ§ДЎдіМгЕФЫљгааТЪ§жЎКЭЮЊЃК![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
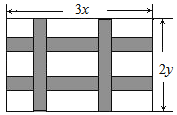
ЁОЬтФПЁПШчЭМЃЌвЊЩшМЦвЛЗљГЄЮЊ3xcmЃЌПэЮЊ2ycmЕФГЄЗНаЮЭМАИЃЌЦфжагаСНКсСНЪњЕФВЪЬѕЃЌКсВЪЬѕЕФПэЖШЮЊacmЃЌЪњВЪЬѕЕФПэЖШЮЊbcmЃЌЮЪПеАзЧјгђЕФУцЛ§ЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМдкжа![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФЦНЗжЯпЃЌНЛ
ЕФЦНЗжЯпЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() .
.
ЧѓжЄЃКЃЈ1ЃЉ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉ![]() ЮЊЕШбќШ§НЧаЮ
ЮЊЕШбќШ§НЧаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
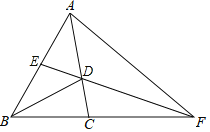
ЁОЬтФПЁПШчЭМЃЌдкЯТСаЬѕМўжаЃЌВЛФмжЄУїЁїABDЁеЁїACDЕФЪЧЃЈ ЃЉ.

A.BD=DCЃЌ AB=AC B.ЁЯADB=ЁЯADCЃЌBD=DC
C.ЁЯB=ЁЯCЃЌЁЯBAD=ЁЯCAD D. ЁЯB=ЁЯCЃЌBD=DC
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌНЋзјБъдЕуOбиxжсЯђзѓЦНвЦ2ИіЕЅЮЛГЄЖШЕУЕНЕуAЃЌЙ§ЕуAзїyжсЕФЦНааЯпНЛЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓгкЕуBЃЌAB=
ЕФЭМЯѓгкЕуBЃЌAB=![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєPЃЈx1ЃЌy1ЃЉЁЂQЃЈx2ЃЌy2ЃЉЪЧИУЗДБШР§КЏЪ§ЭМЯѓЩЯЕФСНЕуЃЌЧвx1ЃМx2ЪБЃЌy1ЃОy2ЃЌжИГіЕуPЁЂQИїЮЛгкФФИіЯѓЯоЃПВЂМђвЊЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃН2xЃЋ6гыЗДБШР§КЏЪ§yЃН![]() (kЃО0)ЕФЭМЯѓНЛгкЕуA(1ЃЌm)ЃЌгыxжсНЛгкЕуBЃЌЦНаагкxжсЕФжБЯпyЃНn(0ЃМnЃМ6)НЛЗДБШР§КЏЪ§ЕФЭМЯѓгкЕуMЃЌНЛABгкЕуNЃЌСЌНгBM.
(kЃО0)ЕФЭМЯѓНЛгкЕуA(1ЃЌm)ЃЌгыxжсНЛгкЕуBЃЌЦНаагкxжсЕФжБЯпyЃНn(0ЃМnЃМ6)НЛЗДБШР§КЏЪ§ЕФЭМЯѓгкЕуMЃЌНЛABгкЕуNЃЌСЌНгBM.
(1)ЧѓmЕФжЕКЭЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
(2)жБЯпyЃНnбиyжсЗНЯђЦНвЦЃЌЕБnЮЊКЮжЕЪБЃЌЁїBMNЕФУцЛ§ЮЊ![]() ЃП
ЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
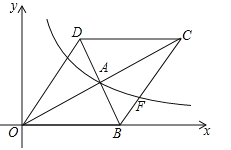
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌСтаЮOBCDЕФБпOBдкxжсЩЯЃЌЗДБШР§КЏЪ§![]() ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§СтаЮЖдНЧЯпЕФНЛЕуAЃЌЧвгыБпBCНЛгкЕуFЃЌЕуAЕФзјБъЮЊЃЈ4ЃЌ2ЃЉЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓОЙ§СтаЮЖдНЧЯпЕФНЛЕуAЃЌЧвгыБпBCНЛгкЕуFЃЌЕуAЕФзјБъЮЊЃЈ4ЃЌ2ЃЉЃЎ
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЧѓЕуFЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПABЁЮCDЃЌOEЦНЗжЁЯBOCЃЌOFЁЭOEЃЌOPЁЭCDЃЌЁЯABO=aЁуЃЎдђЯТСаНсТлЃК ЂйЁЯBOE=![]() ЃЈ180ЉaЃЉЁуЃЛЂкOFЦНЗжЁЯBODЃЛЂлЁЯPOE=ЁЯBOFЃЛЂмЁЯPOB=2ЁЯDOFЃЎЦфжае§ШЗНсТл__________ЃЈЬюБрКХЃЉЃЎ
ЃЈ180ЉaЃЉЁуЃЛЂкOFЦНЗжЁЯBODЃЛЂлЁЯPOE=ЁЯBOFЃЛЂмЁЯPOB=2ЁЯDOFЃЎЦфжае§ШЗНсТл__________ЃЈЬюБрКХЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
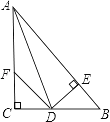
ЁОЬтФПЁПШчЭМЃКдкЁїABCжаЃЌЁЯC=90ЁуЃЌADЪЧЁЯBACЕФЦНЗжЯпЃЌDEЁЭABгкEЃЌFдкACЩЯЃЌBD=DFЃЛ
ЧѓжЄЃКЃЈ1ЃЉCF=EBЃЎ
ЃЈ2ЃЉAB=AF+2EBЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com