
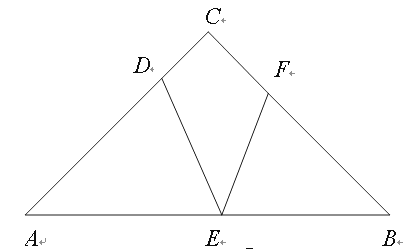
.如图,在Rt△ABC中,∠C=90°,AC=BC=4cm,点D为AC边上一点,且AD=3cm,动点E从点A出发,以1cm/s的速度沿线段AB向终点B运动,运动时间为x s.作∠DEF=45°,与边BC相交于点F.设BF长为y cm.
cm.
(1)当x= s时,DE ⊥AB;
⊥AB;
(2)求在点E运动过程中,y与x之间的函数关系式及点F运动路线的长;
(3)当△BEF为等腰三角 形
形 时,求x的值.
时,求x的值.


解:(1)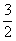

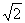
 2分
2分
(2)∵在△ABC中,∠C=90°,AC=B C=4.
C=4.
∴∠A=∠B=45°,AB=4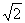
 ,∴∠ADE+∠AED=135°;
,∴∠ADE+∠AED=135°;
又∵∠D EF=45°,∴∠BEF+∠AED=135°,∴∠ADE=∠BEF;
EF=45°,∴∠BEF+∠AED=135°,∴∠ADE=∠BEF;
∴△ADE∽△BEF 4分
∴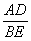
 =
=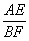
 ,
,
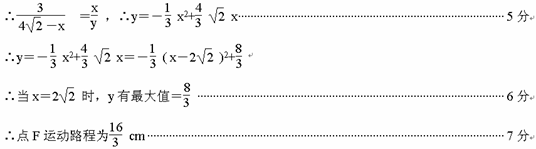

(3)这里有三种情况:
①如图,若EF=BF,则∠B=∠BEF;


又∵△ADE∽△BEF,∴∠A=∠ADE=45°
∴∠AED=90°,∴AE=DE=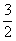

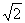
 ,
,
∵动点E的速度为1cm/s ,∴
,∴ 此时x=
此时x=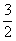

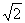
 s;
s;
②如图,若EF=BE,则∠B=∠EFB
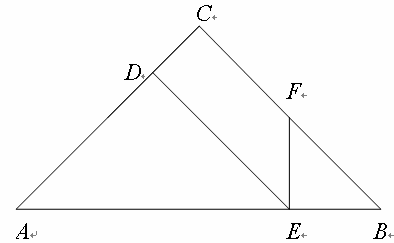

又∵△ADE∽△BEF,∴∠A=∠AED=45°
∴∠ADE=90°,∴AE=3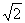
 ,
,
∵动点E的速度为1cm/s
∴此时x=3
 s;
s;
③如图,若BF=BE,则∠FEB=∠EFB;




 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
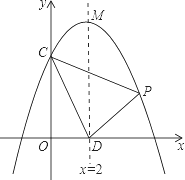
如图,在平面直角坐标系xOy中,抛物线 交y轴于点C,对称轴与x轴交于点D, 设点P(x,y)是该抛物线在x轴上方的一个动点(与点C不重合),△PCD的面积为S,求S关于x的函数关系式,并写出自变量x的取值范围。
交y轴于点C,对称轴与x轴交于点D, 设点P(x,y)是该抛物线在x轴上方的一个动点(与点C不重合),△PCD的面积为S,求S关于x的函数关系式,并写出自变量x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,A、B两点的坐标分别是(8,0)、(0,6),点P由点B出发沿BA方向向点A作匀速直线运动,速度为每秒3个单位长度,点Q由A出发沿AO(O为坐标原点)方向向点O作匀速直线 运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<
运动,速度为每秒2个单位长度,连接PQ,若设运动时间为t(0<t<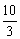
 )秒
)秒 .解答如下问题:
.解答如下问题:


(1)当t为何值 时,PQ∥BO?
时,PQ∥BO?
(2)设△AQP的面积为S,
①求S与t之间的函数关系式,并求出S的最大值;
② 若我们规定:点P、Q的坐标分别为(x1,y1),(x2,y2),则新坐标(x2﹣x1,y2﹣y1)称为“向量PQ”的坐标.当S取最大值时,求“向量PQ”的坐标.
若我们规定:点P、Q的坐标分别为(x1,y1),(x2,y2),则新坐标(x2﹣x1,y2﹣y1)称为“向量PQ”的坐标.当S取最大值时,求“向量PQ”的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在 边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿折线BC﹣CD向点D运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动,设点F的运动时间为t秒.
边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿折线BC﹣CD向点D运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动,设点F的运动时间为t秒.
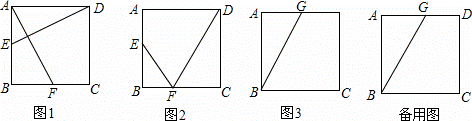

(1)点F在边BC上.
①如图1,连接DE,AF,若DE⊥AF,求t的值;
②如图2,连结EF,DF,当t为何值时,△EBF与△DCF相似?
(2)如图3,若点G是边AD的中点,BG,EF相交于点O,试探究:是否存在在某一时刻t,使得
 ?若存在,求出t
?若存在,求出t 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,A
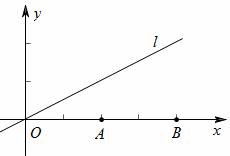
如图,在平面直角坐标系xOy中,A (2,0),B(4,0),动点C在直线
(2,0),B(4,0),动点C在直线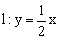 上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是【 】
上,若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是【 】
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,Rt△ABC中,∠ACB=90°,AC=BC=4cm,CD=1cm,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,至A点结束,设E点的运动时间为t秒,连接DE,当△BDE是直角三角 形时,t的值为 秒。
形时,t的值为 秒。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在直角坐标系中,点A的坐标为(8,0),点 B(t,b)在直线y=b上运动,点D、E、F分别为OB、OA、AB的中点,其中b是大于零的常数。设直线y=b与y轴交于点C,问:四边形DEFB能不能是矩形?若能,求出t的值;若不能,说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将△ABC绕着点C顺时针旋转一定角度后得到△A′B′C′,若∠A=40°.∠B′=110°,∠BCA′=80°,则旋转角的度数是【 】
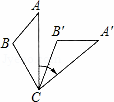
A.110° B.80° C.50°  D.30°
D.30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com