练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

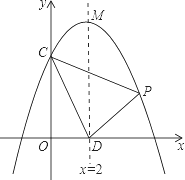
    如图，在平面直角坐标系xOy中，抛物线交y轴于点C，对称轴与x轴交于点D， 设点P（x，y）是该抛物线在x轴上方的一个动点（与点C不重合），△PCD的面积为S，求S关于x的函数关系式，并写出自变量x的取值范围。


    令，即，解得。

    设抛物线与x轴交于点A、B，（点A在点B的左边），则A（，0）、B（，0）。

    ②当点P在CM之间时，即0＜x≤2，如答图2，

    ∵P（x，y），且点P在第一象限，∴PE=y，OE=x。

    ∴。

    ∴。

    将代入上式得：。

    综上所述，S关于x的函数关系式为：。

    【考点】动点问题，抛物线与x的交点问题，解一元二次方程，由实际问题列函数关系式，分类思想和转换思想的应用。


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，某商场设立了一个可以自由转动的转盘，并规定：顾客购物10元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品．下表是活动进行中的一组统计数据：

    （1）计算并完成表格：

    （2）请估计，当n很大时，频率将会接近多少？

    （3）假如你去转动转盘一次，你获得铅笔的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图①是3×3菱形格，将其中两个格子涂黑，并且使得涂黑后的整个图案是轴对称图形，约定绕菱形ABCD的中心旋转能重合的图案都视为同一种，例②中四幅图就视为同一种，则得到不同共有【    】

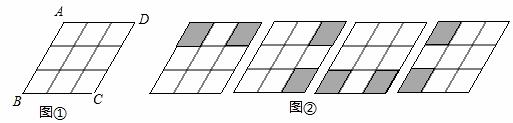
     A．4种         B．5种        C．6种        D．7种

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     如图，平面直角坐标系中，⊙O半径长为1.点⊙P（a，0），⊙P的半径长为2，把⊙P向左平移，当⊙P与⊙O相交时，a值的取值范围为         。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


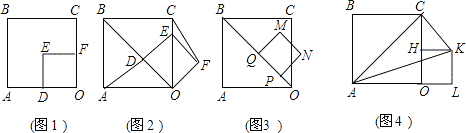
    如图1，把边长分别是为4和2的两个正方形纸片OABC和OD′E′F′叠放在一起．

    （1）操作1：固定正方形OABC，将正方形OD′E′F′绕点O按顺时针方向旋转45°得到正方形ODEF，如图2，连接AD、CF，线段AD与CF之间有怎样的数量关系？试证明你的结论；

    （2）操作2，如图2，将正方形ODEF沿着射线DB以每秒1个单位的速度平移，平移后的正方形ODEF设为正方形PQMN，如图3，设正方形PQMN移动的时间为x秒，正方形PQMN与正方形OABC的重叠部分面积为y，直接写出y与x之间的函数解析式；

    （3）操作3：固定正方形OABC，将正方形OD′E′F′绕点O按顺时针方向旋转90°得到正方形OHKL，如图4，求△ACK的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


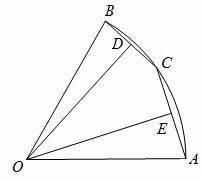
    如图，在半径为2的扇形AOB中，∠AOB=60°，点C是弧AB上的一个动点（不与点A、B重合）OD⊥BC，OE⊥AC，垂足分别为D、E．

    （1）当BC=1时，求线段OD的长；

    （2）在△DOE中是否存在长度保持不变的边？如果存在，请指出并求其长度，如果不存在，请说明理由；

    （3）设BD=x，△DOE的面积为y，求y关于x的函数关系式，并写出它的定义域。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图1，在平面直角坐标系中，直线AB与轴交于点A，与轴交于点B，与直线OC：交于点C．

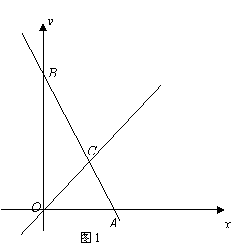
    （1）若直线AB解析式为，

    ①求点C的坐标；

    ②求△OAC的面积．

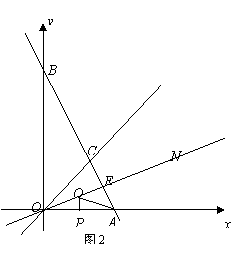
    （2）如图2，作的平分线ON，若AB⊥ON，垂足为E， OA＝4，P、Q分别为线段OA、OE上的动点，连结AQ与PQ，试探索AQ＋PQ是否存在最小值？若存在，求出这个最小值；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，四边形ABCD是平行四边形，过点A、C、D作抛物线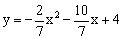，与x轴的另一交点为E，连结CE。

    （1）求点A、B、C、D的坐标；

    （2）已知抛物线的对称轴l交x轴于点F，交线段CD于点K，点M、N分别是直线l和x轴上的动点，连结MN，当线段MN恰好被BC垂直平分时，求点N的坐标；

    （3）在满足（2）的条件下，过点M作一条直线，使之将四边形ABCD的面积分为2：3的两部分，设该直线与x轴交于点P，求点P的坐标。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    .如图，在Rt△ABC中，∠C=90°，AC=BC=4cm，点D为AC边上一点，且AD=3cm，动点E从点A出发，以1cm/s的速度沿线段AB向终点B运动，运动时间为x s．作∠DEF=45°，与边BC相交于点F．设BF长为ycm．

    （1）当x=     s时，DE⊥AB；

    （2）求在点E运动过程中，y与x之间的函数关系式及点F运动路线的长；

    （3）当△BEF为等腰三角形时，求x的值．

    查看答案和解析>>

    同步练习册答案