练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，已知AB∥CD，PA、PC分别平分∠BAC和∠ACD，试判断△APC的形状，并说明理由．
    考点：平行线的性质
    专题：
    分析：由平行线的性质和角平分线的定义可求得∠1+∠2=90°，可判定△APC的形状．
    解答：解：△APC为直角三角形，理由如下：
    ∵AB∥CD，
    ∴∠BAC+∠DCA=180°，
    ∵PA、PC分别平分∠BAC和∠ACD，
    ∴∠BAC=2∠1，∠DCA=2∠2，
    ∴2∠1+2∠2=180°，
    ∴∠1+∠2=90°，
    ∴∠APC=90°，即△APC为直角三角形．
    点评：本题主要考查平行线的性质，掌握平行线的性质是解题的关键，即①两直线平行?同位角相等，②两直线平行?内错角相等，③两直线平行?同旁内角互补．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

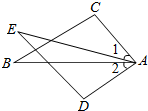    如图，已知∠1=∠2，AC=AD，增加下列条件之一：①AB=AE；②BC=ED；③∠C=∠D；④∠B=∠E．其中能使△ABC≌△AED的条件有（　　）
    A、1个B、2个C、3个D、4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

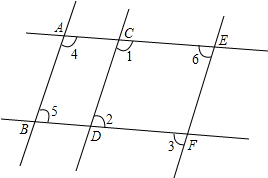    如图，请分别根据已知条件进行推理，得出结论，并在括号内注明理由．
    （1）∵∠2=∠3（已知），
    ∴
     
    ∥
     
    （
     
    　）
    （2）∵∠2=∠5（已知），
    ∴
     
    ∥
     
    （
     
    　）
    （3）∵∠2+∠1=180°（已知），
    ∴
     
    ∥
     
    （
     
    　）
    （4）∵∠5=∠3（已知），
    ∴
     
    ∥
     
    （
     
    　）
    （5）∵∠4+∠6=180°（已知），
    ∴
     
    ∥
     
    （
     
    　）
    （6）∵AB∥CD，AB∥EF（已知），
    ∴
     
    ∥
     
    （
     
    　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，直线a、b、c被直线l所截，如果∠1=∠2=65°，且直线b∥c，那么直线a与c平行吗？∠3等于多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    甲、乙、丙三地的海拔高度分别是20米，-15米和-10米，那么，最高处的地方比最低处的地方高（　　）
    A、35米B、15米
    C、10米D、5米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列图形中，正确表示△ABC中BC边上的高的是（　　）
    A、
    B、
    C、
    D、

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一艘轮船要从A处驶向B处，如图所示，由于受大风影响，轮船一开始就偏离航线9°，航行到C处时发现∠ABC=11°，此时，轮船应把船头调转多少度才能到达B处？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如果x=
    1
    2
    是关于x的方程2x+m=2的解，那么m的值是（　　）
    A、1
    B、
    1
    2
    C、-1
    D、-
    1
    2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    0.1x+0.1
    0.3
    -
    0.3x-0.5
    0.4
    =1．

    查看答案和解析>>

    同步练习册答案