
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,连接
上,连接![]() ,将
,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,若
处,若![]() 有一边垂直
有一边垂直![]() ,则
,则![]() ______.
______.
【答案】![]() 或
或![]()
【解析】
存在2种情况,一种是DE⊥BC,还有一种是DF⊥BC,分别根据折叠的性质求解可得.
情况一:ED⊥BC,如下图
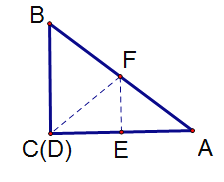
∵![]() ,
,![]() ,
,![]() ,
,
∴BC=3
∵BC⊥DE,
∴点D与点C重合
∴点E是AC的中点,EF⊥AC
∵∠ACB=90°
∴EF∥BC
∴EF是△ABC的中位线
∴EF=![]()
![]()
情况二:DF⊥BC,如下图,过点F作AC的垂线,交AC于点G

∵DF⊥BC
∴DF∥AC,∴∠DFE=∠AEF
由折叠性质得:∠DEF=∠AEF,DE=AE,DF=AF
∴∠DFE=∠DEF
∴DE=DF
∴DE=DF=AF=AE
设DE=x
∵DF∥AC
∴△BDF∽△BCA
∴![]()
代入解得:BD=![]()
在Rt△CDE中,![]() ,代入解得:x=
,代入解得:x=![]() 或x=20(舍)
或x=20(舍)
∴AF=![]() ,BD=
,BD=![]() ,∴CD=
,∴CD=![]()
∴FG=CD=![]()
∴在Rt△AGF中,AG=![]()
∴EG=![]()
∴在Rt△EFG中,EF=![]()
故答案为:![]() 或
或![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
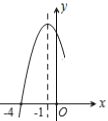
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③一元二次方程
;③一元二次方程![]() 的解是
的解是![]() ,
,![]() ;④当
;④当![]() 时,
时,![]() ,其中正确的结论有__________.
,其中正确的结论有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发市场有中招考试文具套装,其中![]() 品牌的批发价是每套
品牌的批发价是每套![]() 元,
元,![]() 品牌的批发价是每套
品牌的批发价是每套![]() 元,小王需购买
元,小王需购买![]() 两种品牌的文具套装共
两种品牌的文具套装共![]() 套.
套.
(1)若小王按需购买![]() 两种品牌文具套装共用
两种品牌文具套装共用![]() 元,则各购买多少套?
元,则各购买多少套?
(2)凭会员卡在此批发市场购买商品可以获得![]() 折优惠,会员卡费用为
折优惠,会员卡费用为![]() 元.若小王购买会员卡并用此卡按需购买
元.若小王购买会员卡并用此卡按需购买![]() 套文具套装,共用了
套文具套装,共用了![]() 元.设
元.设![]() 品牌文具套装买了
品牌文具套装买了![]() 包,请求出
包,请求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
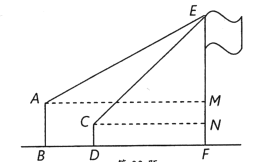
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.6米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.6米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).求旗杆EF的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
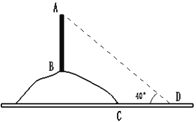
【题目】在坡度为![]() 的山坡
的山坡![]() 上立有一块大型广告牌
上立有一块大型广告牌![]() ,如图,广告牌底部
,如图,广告牌底部![]() 点到山脚
点到山脚![]() 点的距离
点的距离![]() 为20米,某同学在离山坡脚4米的
为20米,某同学在离山坡脚4米的![]() 处(
处(![]() 米)测得广告牌顶部
米)测得广告牌顶部![]() 的仰角为
的仰角为![]() ,求广告牌
,求广告牌![]() 的高度.(结果保留整数,参考数值:
的高度.(结果保留整数,参考数值:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中, BC=8,以AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.
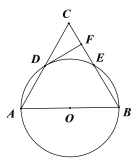
(1)求证:DF为⊙O的切线.
(2)求弧DE的长度.
(3)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c和直线y=kx+b都经过点(﹣1,0),抛物线的对称轴为x=1,那么下列说法正确的是( )
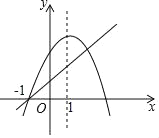
A.ac>0
B.b2﹣4ac<0
C.k=2a+c
D.x=4是ax2+(b﹣k)x+c<b的解
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.

(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com