
【题目】如图,在等边△ABC中, BC=8,以AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.
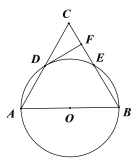
(1)求证:DF为⊙O的切线.
(2)求弧DE的长度.
(3)求EF的长.
【答案】(1)见解析;(2)![]() ;(3)2
;(3)2
【解析】
(1)连接DO,先证出△OAD是等边三角形,故∠ADO=60°,再求出∠CDF,最后证出OD⊥DF,利用切线的判定即可得到.DF为⊙O的切线;
(2)连接OD、OE,先求出∠DOE的度数,再代入弧长公式即可;
(3)先求出CD的长,再求CF的长,利用EF=BC-CF-BE即可.
(1)证明:连接DO,

∵△ABC是等边三角形,
∴∠A=∠C=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴∠ADO=60°,
∵DF⊥BC,
∴∠CDF=90°﹣∠C=30°,
∴∠FDO=180°﹣∠ADO﹣∠CDF=90°,
即OD⊥DF,
∵OD为半径,
∴DF为⊙O的切线;
(2)连接OD、OE
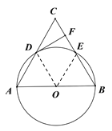
∵EO=OB,∠EOB=60°
∴△OBE是等边三角形,
∴∠EOB =60°
∴∠DOE=180°-∠EOB-AOD=60°
∵AB=BC=8
∴![]() 的半径为4
的半径为4
∴![]()
(3)解:∵△OAD是等边三角形,
∴AD=AO=![]() AB=4,
AB=4,
∴CD=AC﹣AD=4,
Rt△CDF中,∠CDF=30°,
∴CF=![]() CD=2,DF=2
CD=2,DF=2![]() ,
,
连接OE,
∵OB=OE,∠B=60°,
∴△OBE是等边三角形,
∴OB=BE=4,
∴EF=BC﹣CF﹣BE=8﹣2﹣4=2;


科目:初中数学 来源: 题型:
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图(1)所示,成本y2与销售月份之间的关系如图(2)所示(图(1)的图象是线段图(2)的图象是抛物线)
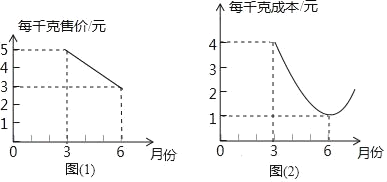
(1)分别求出y1、y2的函数关系式(不写自变量取值范围);
(2)通过计算说明:哪个月出售这种蔬菜,每千克的收益最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=![]() ,AD=3,点E从点B出发,沿BC边运动到点C,连结DE,点E作DE的垂线交AB于点F.在点E的运动过程中,以EF为边,在EF上方作等边△EFG,则边EG的中点H所经过的路径长是( )
,AD=3,点E从点B出发,沿BC边运动到点C,连结DE,点E作DE的垂线交AB于点F.在点E的运动过程中,以EF为边,在EF上方作等边△EFG,则边EG的中点H所经过的路径长是( )

A. 2 ![]() B. 3
B. 3![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2![]() ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为________.
,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
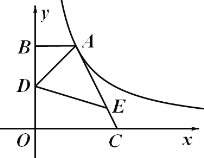
【题目】如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,
点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE
的面积为3,则k的值为 ▲ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.

(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA= °时,四边形BFDE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,动点M从点B出发沿线段
,动点M从点B出发沿线段![]() 以每秒2个单位长度的速度向终点C运动;动点N同时从点C出发沿线段
以每秒2个单位长度的速度向终点C运动;动点N同时从点C出发沿线段![]() 以每秒1个单位长度的速度向终点D运动,设运动的时间为
以每秒1个单位长度的速度向终点D运动,设运动的时间为![]() .
.
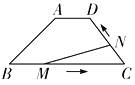
(1)求![]() 的长.
的长.
(2)当![]() 时,求t的值
时,求t的值
(3)试探究:t为何值时,![]() 为等腰三角形?
为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程,为了解学生对这四门校本课程的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制了(图1)、(图2)两幅均不完整的统计图.
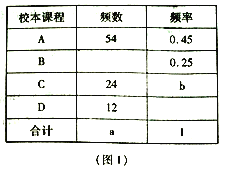
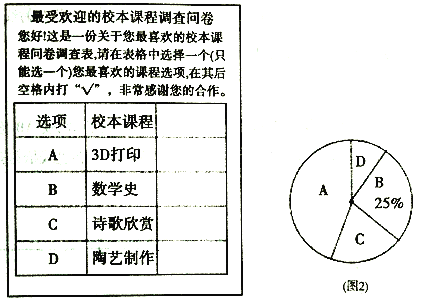
请您根据图中提供的信息回答下列问题:
(1)统计图中的a= ,b= ;
(2)“D”对应扇形的圆心角为 度;
(3)根据调查结果,请您估计该校1200名学生中最喜欢“数学史”校本课程的人数;
(4)小明和小亮参加校本课程学习,若每人从“A”、“B”、“C”三门校本课程中随机选取一门,请用画树状图或列表格的方法,求两人恰好选中同一门校本课程的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com