
如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.

(1)求证:△ACD≌△BCE;
(2)若AC=3cm,则BE= ( )cm。
(1)见解析 (2)6
【解析】(1)证明:∵△CDE是等腰直角三角形,∠DCE=90°,
∴CD=CE,
∵∠ACB=90°,
∴∠ACB=∠DCE,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中
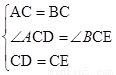 ,
,
∴△ACD≌△BCE(SAS);
(2)【解析】
∵AC=BC=3,∠ACB=90°,由勾股定理得:AB=3 cm.
cm.
又∵DB=AB,
∴AD=2AB=6 cm.,
cm.,
∵△ACD≌△BCE;
∴BE=AD=6 cm.,
cm.,
故答案为:6 cm..
cm..
(1)求出∠ACD=∠BCE,根据SAS推出两三角形全等即可;
(2)根据全等得出AD=BE,根据勾股定理求出AB,即可求出AD,代入求出即可.


科目:初中数学 来源:2014中考名师推荐数学图形的折叠(解析版) 题型:选择题
如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在点A′、D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,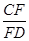 的值为( )
的值为( )
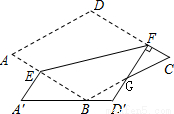
A.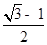
B.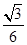 C.
C.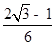
D.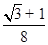
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学二次函数(解析版) 题型:选择题
二次函数y=x2的图象向上平移2个单位,得到新的图象的二次函数表达式是( )
A.y=x2-2
B.y=(x-2)2
C.y=x2+2
D.y=(x+2)2
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(二)(解析版) 题型:填空题
在一张直角三角形纸片中,分别沿两直角边上一点与斜边中点的连线剪去两个三角形,得到如图所示的直角梯形,则原直角三角形纸片的斜边长是 ( )

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(二)(解析版) 题型:选择题
如图,若∠A=60°,AC=20m,则BC大约是(结果精确到0.1m) ( )

A.34.64m B.34.6m C.28.3m D.17.3m
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(一)(解析版) 题型:选择题
一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )

A.90° B.100° C.130° D.180°
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省大庆市九年级下学期期末数学试卷(解析版) 题型:解答题
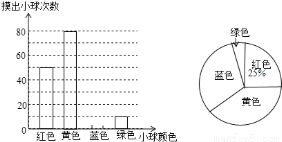
一个不透明的口袋装有若干个红、黄、蓝、绿四种颜色的小球,小球除颜色外完全相同,为估计该口袋中四种颜色的小球数量,每次从口袋中随机摸出一球记下颜色并放回,重复多次试验,汇总实验结果绘制如图不完整的条形统计图和扇形统计图.
根据以上信息解答下列问题:
(1)求实验总次数,并补全条形统计图;
(2)扇形统计图中,摸到黄色小球次数所在扇形的圆心角度数为多少度?
(3)已知该口袋中有10个红球,请你根据实验结果估计口袋中绿球的数量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com