
ΓΨΧβΡΩΓΩΈ“ – Β ©≥«œγ…ζΜνά§ΜχΖ÷άύΙήάμΘ§ΆΤΫχ…ζΧ§ΈΡΟςΫ®…η. ΈΣ‘ω«Ω―ß…ζΒΡΜΖ±Θ“β ΕΘ°ΥφΜζ≥ι»Γ8Οϊ―ß…ζΘ§Ε‘ΥϊΟ«ΒΡά§ΜχΖ÷άύΆΕΖ≈«ιΩωΫχ––Βς≤ιΘ§’β8Οϊ―ß…ζΖ÷±π±ξΦ«ΈΣAΘ§BΘ§CΘ§DΘ§EΘ§FΘ§GΘ§HΘ§Τδ÷–ΓΑΓΧΓ±±μ ΨΆΕΖ≈’ΐ»ΖΘ§ΓΑΓΝΓ±±μ ΨΆΕΖ≈¥μΈσΘ§Ά≥ΦΤ«ιΩω»γœ¬±μΘ°

Δ≈ «σ8Οϊ―ß…ζ÷–÷Ν…Ό”–»ΐάύά§ΜχΆΕΖ≈’ΐ»ΖΒΡΗ≈¬ ΘΜ
ΔΤ ΈΣΫχ“Μ≤ΫΝΥΫβά§ΜχΖ÷άύΆΕΖ≈«ιΩωΘ§œ÷¥”8Οϊ―ß…ζάοΓΑ”–ΚΠά§ΜχΓ±ΆΕΖ≈¥μΈσΒΡ―ß…ζ÷–ΥφΜζ≥ι»ΓΝΫ»ΥΫ” ή≤…ΖΟΘ§ ‘”Ο±ξΦ«ΒΡΉ÷ΡΗΝ–ΨΌΥυ”–Ω…Ρή≥ι»ΓΒΡΫαΙϊΘ§≤Δ«σ≥ωΗ’ΚΟ≥ιΒΫCΓΔGΝΫΈΜ―ß…ζΒΡΗ≈¬ Θ°
ΓΨ¥πΑΗΓΩΔ≈ P=![]() ΘΜΔΤ
ΘΜΔΤ ![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©÷±Ϋ”άϊ”ΟΗ≈¬ ΙΪ Ϋ«σΫβΩ…ΒΟΘΜ
Θ®2Θ©άϊ”ΟΝ–±μΖ®Ω…ΒΟΥυ”–Β»Ω…ΡήΫαΙϊΘ§¥”÷–’“ΒΫΖϊΚœΧθΦΰΒΡΫαΙϊ ΐΘ§‘ΌΗυΨίΗ≈¬ ΙΪ Ϋ«σΫβΩ…ΒΟΘ°
Δ≈ ΓΏ”–12ΗωΒ»Ω…ΡήΫαΙϊΘ§―ΓΒΫ÷Ν…Ό”–»ΐάύά§ΜχΆΕΖ≈’ΐ»ΖΒΡΫαΙϊ”–5ΗωΘ§
Γύ8Οϊ―ß…ζ÷–÷Ν…Ό”–»ΐάύά§ΜχΆΕΖ≈’ΐ»ΖΒΡΗ≈¬ ΈΣ P=![]() ΘΜ
ΘΜ
ΔΤ Ν–±μ»γœ¬ΘΚ
A | C | F | G | |
A | CA | FA | GA | |
C | AC | FC | GC | |
F | AF | CF | GF | |
G | AG | CG | FG |
”–12ΗωΒ»Ω…ΡήΫαΙϊΘ§Η’ΚΟ≥ιΒΫCΓΔGΒΡΫαΙϊ”–2ΗωΘ§
ΓύP=![]() .
.
ΓύΗ’ΚΟ≥ιΒΫCΓΔGΒΡΗ≈¬ ΈΣ![]() ΘΜ
ΘΜ


 –Γ―ßΩΈ ±ΧΊ―ΒœΒΝ–¥πΑΗ
–Γ―ßΩΈ ±ΧΊ―ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΆθάœ ΠΈΣΝΥΫβΆ§―ßΟ«Ε‘Ϋπ”ΙΈδœά–ΓΥΒΒΡ‘ΡΕΝ«ιΩωΘ§ΥφΜζΕ‘≥θ»ΐΡξΦΕΒΡ≤ΩΖ÷Ά§―ßΫχ––Βς≤ιΘ§ΫΪΒς≤ιΫαΙϊΖ÷≥…“‘œ¬ΈεάύΘΚAΘΚΩ¥Ιΐ0ΓΪ3±ΨΘ§BΘΚΩ¥Ιΐ4ΓΪ6±ΨΘ§CΘΚΩ¥Ιΐ7ΓΪ9±ΨΘ§DΘΚΩ¥Ιΐ10ΓΪ12±ΨΘ§EΘΚΩ¥Ιΐ13ΓΪ15±Ψ.≤ΔΗυΨίΒς≤ιΫαΙϊΜφ÷ΤΝΥ»γΆΦ1ΓΔΆΦ2ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ°
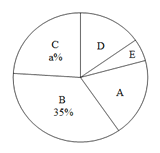
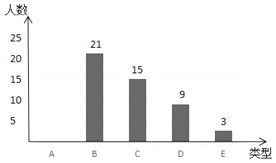
(1)ΆΦ2÷–ΒΡa = Θ§DΥυΕ‘ΒΡ‘≤–ΡΫ«Ε» ΐΈΣ ΓψΘΜ
(2)«κ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
(3)±Ψ¥ΈΒς≤ι÷–Eάύ”–2Ρ–1≈°Θ§Άθάœ Πœκ¥”÷–≥ι»Γ2ΟϊΆ§―ßΖ÷±πΉΪ–¥“ΜΤΣΕΝ ι± Φ«Θ°«κ”ΟΝ–±μΜρΜ≠ ςΉ¥ΆΦΒΡΖΫΖ®«σΥυ≥ι»ΓΒΡΝΫΟϊ―ß…ζ«ΓΚΟ «“ΜΡ–“Μ≈°ΒΡΗ≈¬ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΒψA1ΒΡΉχ±ξΈΣ(0Θ§1)Θ§ΒψA2‘Ύx÷αΒΡ’ΐΑκ÷α…œΘ§«“ΓœA1A2OΘΫ30ΓψΘ§ΙΐΒψA2ΉςA2A3ΓΆA1A2Θ§ΫΜy÷α”ΎΒψA3ΘΜΙΐΒψA3ΉςA3A4ΓΆA2A3Θ§ΫΜx÷α”ΎΒψA4ΘΜΙΐΒψA4ΉςA4A5ΓΆA3A4Θ§ΫΜy÷α”ΎΒψA5ΘΜΓ≠Γ≠ΘΜΑ¥¥ΥΙφ¬…Ϋχ––œ¬»ΞΘ§‘ρΒψA2021ΒΡΉχ±ξΈΣΘ® Θ©
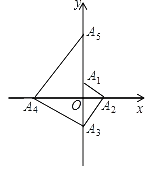
A.(0Θ§31011)B.(©¹31011Θ§0)C.(0Θ§31010)D.(©¹31010Θ§0)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ”–Ή®Φ“÷Η≥ωΘΚ»ΥΈΣ–ΆΩ’ΤχΈέ»ΨΘ®»γΤϊ≥ΒΈ≤Τχ≈≈Ζ≈Β»Θ© «Έμω≤ΧλΤχΒΡ÷Ί“Σ≥…“ρΘ°Ρ≥–ΘΈΣ≥Ϊ“ιΓΑΟΩ»Υ…ΌΩΣ“ΜΧλ≥ΒΘ§Ι≤Ϋ®¬Χ…ΪΦ“‘ΑΓ±Θ§œκΝΥΫβ―ß…ζ…œ―ßΒΡΫΜΆ®ΖΫ ΫΘ°Ψ≈ΡξΦΕΘ®8Θ©ΑύΒΡ5ΟϊΆ§―ßΝΣΚœ…ηΦΤΝΥ“ΜΖίΒς≤ιΈ ΨμΘ°Ε‘ΗΟ–Θ≤ΩΖ÷―ß…ζΫχ––ΝΥΥφΜζΒς≤ιΘ°Α¥AΘ®ΤοΉ‘––≥ΒΘ©ΓΔBΘ®≥ΥΙΪΫΜ≥ΒΘ©ΓΔCΘ®≤Ϋ––Θ©ΓΔDΘ®≥ΥΥΫΦ“≥ΒΘ©ΓΔEΘ®ΤδΥϊΖΫ ΫΘ©…η÷Ο―ΓœνΘ§“Σ«σ±ΜΒς≤ιΆ§―ߥ”÷–ΒΞ―ΓΘ°≤ΔΫΪΒς≤ιΫαΙϊΜφ÷Τ≥…Χθ–ΈΆ≥ΦΤΆΦ1ΚΆ…»–ΈΆ≥ΦΤΆΦ2Θ§ΗυΨί“‘…œ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©±Ψ¥ΈΫ” ήΒς≤ιΒΡΉή»Υ ΐ «ΓΓ ΓΓ»ΥΘ§…»–ΈΆ≥ΦΤΆΦ÷–ΓΑΤοΉ‘––≥ΒΓ±Υυ‘Ύ…»–ΈΒΡ‘≤–ΡΫ«Ε» ΐ «ΓΓ ΓΓΕ»Θ§«κ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®2Θ©“―÷Σ’β5Οϊ―ß…ζ÷–”–2Οϊ≈°Ά§―ßΘ§“Σ¥”’β5Οϊ―ß…ζ÷–»Έ―ΓΝΫΟϊΆ§―ßΜψ±®Βς≤ιΫαΙϊΘ°«κ”ΟΝ–±μΖ®ΜρΜ≠ ςΉ¥ΆΦΒΡΖΫΖ®Θ§«σ≥ω«ΓΚΟ―Γ≥ω1ΟϊΡ–…ζΚΆ1Οϊ≈°…ζΒΡΗ≈¬ Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
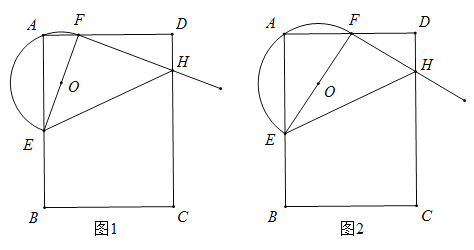
ΓΨΧβΡΩΓΩ“―÷Σ:‘ΎΨΊ–Έ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Ζ÷±π «±Ώ
Ζ÷±π «±Ώ![]() Θ§
Θ§![]() …œΒΡΒψΘ§ΙΐΒψ
…œΒΡΒψΘ§ΙΐΒψ![]() Ής
Ής![]() ΒΡ¥ΙœΏΫΜ
ΒΡ¥ΙœΏΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§“‘
Θ§“‘![]() ΈΣ÷±ΨΕΉςΑκ‘≤
ΈΣ÷±ΨΕΉςΑκ‘≤![]() Θ°
Θ°
Θ®1Θ©ΧνΩ’ΘΚΒψ![]() _____________Θ®ΧνΓΑ‘ΎΓ±ΜρΓΑ≤Μ‘ΎΓ±Θ©
_____________Θ®ΧνΓΑ‘ΎΓ±ΜρΓΑ≤Μ‘ΎΓ±Θ©![]() …œΘΜΒ±
…œΘΜΒ±![]() ±Θ§
±Θ§![]() ΒΡ÷Β «_____________ΘΜ
ΒΡ÷Β «_____________ΘΜ
Θ®2Θ©»γΆΦ1Θ§‘Ύ![]() ÷–Θ§Β±
÷–Θ§Β±![]() ±Θ§«σ÷ΛΘΚ
±Θ§«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
Θ®3Θ©»γΆΦ2Θ§Β±![]() ΒΡΕΞΒψ
ΒΡΕΞΒψ![]() «±Ώ
«±Ώ![]() ΒΡ÷–Βψ ±Θ§«κ÷±Ϋ”–¥≥ω
ΒΡ÷–Βψ ±Θ§«κ÷±Ϋ”–¥≥ω![]() »ΐΧθœΏΕΈΒΡ ΐΝΩΙΊœΒΘ°
»ΐΧθœΏΕΈΒΡ ΐΝΩΙΊœΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥…δΜς‘ΥΕ·‘±‘Ύ―ΒΝΖ÷–…δΜςΝΥ10¥ΈΘ§≥…Φ®»γΆΦΘ§œ¬Ν–Ϋα¬έ’ΐ»ΖΒΡ «Θ® Θ©
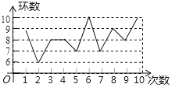
A.ΤΫΨυ ΐ «8B.÷Ύ ΐ «8 C.÷–ΈΜ ΐ «9 D.ΖΫ≤ν «1
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ≤η“Ε «Α≤Μ’ Γ÷ς“ΣΨ≠ΦΟΉςΈο÷°“ΜΘ§2020Ρξ–¬≤η…œ –ΤΎΦδΘ§Ρ≥≤η≥ßΈΣΜώΒΟΉν¥σάϊ“φΘ§ΗυΨί –≥Γ––«ιΘ§Α―–¬≤ηΦέΗώΕ®ΈΣ400‘Σ/kgΘ§≤ΔΗυΨίάζΡξΒΡœύΙΊ ΐΨί’ϊάμ≥ωΒΎxΧλΘ®1ΓήxΓή15Θ§«“xΈΣ’ϊ ΐΘ©÷Τ≤η≥…±ΨΘ®Κ§≤…’ΣΚΆΦ”ΙΛΘ©ΚΆ÷Τ≤ηΝΩΒΡœύΙΊ–≈œΔ»γœ¬±μΘ°ΦΌΕ®ΗΟ≤η≥ßΟΩΧλ÷ΤΉςΚΆœζ έΒΡ–¬≤ηΟΜ”–Υπ ßΘ§«“Ρή‘ΎΒ±Χλ»Ϊ≤Ω έ≥ωΘ®Β±Χλ ’»κ=»’œζ έΕν-»’÷Τ≤η≥…±ΨΘ©
÷Τ≤η≥…±ΨΘ®‘Σ/kgΘ© | 150+10x |
÷Τ≤ηΝΩΘ®kgΘ© | 40+4x |
Θ®1Θ©«σ≥ωΗΟ≤η≥ßΒΎ10ΧλΒΡ ’»κΘΜ
Θ®2Θ©…ηΗΟ≤η≥ßΒΎxΧλΒΡ ’»κΈΣyΘ®‘ΣΘ©Θ° ‘«σ≥ωy”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ≥ωyΒΡΉν¥σ÷ΒΦΑ¥Υ ±xΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
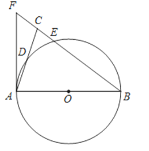
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§BA=BCΘ§“‘ABΈΣ÷±ΨΕΒΡΓ―OΖ÷±πΫΜACΘ§BC”ΎΒψDΘ§EΘ§BCΒΡ―”≥ΛœΏ”κΓ―OΒΡ«–œΏAFΫΜ”ΎΒψFΘ°
Θ®1Θ©«σ÷ΛΘΚΓœABC=2ΓœCAFΘΜ
Θ®2Θ©»τAC=2![]() Θ§CEΘΚEB=1ΘΚ4Θ§«σCEΘ§AFΒΡ≥ΛΘ°
Θ§CEΘΚEB=1ΘΚ4Θ§«σCEΘ§AFΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
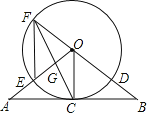
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςOAB÷–Θ§OAΘΫOBΘ§CΈΣAB÷–ΒψΘ§“‘OΈΣ‘≤–ΡΘ§OC≥ΛΈΣΑκΨΕΉς‘≤Θ§AO”κΓ―OΫΜ”ΎΒψEΘ§÷±œΏOB”κΓ―OΫΜ”ΎΒψFΚΆDΘ§Ν§Ϋ”EFΘ°CFΘ§CF”κOAΫΜ”ΎΒψGΘ°
Θ®1Θ©«σ÷ΛΘΚ÷±œΏAB «![]() ΒΡ«–œΏΘΜ
ΒΡ«–œΏΘΜ
Θ®2Θ©«σ÷ΛΘΚODEGΘΫOGEFΘΜ
Θ®3Θ©»τABΘΫ4BDΘ§«σsinAΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com