

分析 (1)由两对角相等(∠APQ=∠C,∠A=∠A),证明△AQP∽△ABC;
(2)当△PQB为等腰三角形时,有两种情况,需要分类讨论.
(I)当点P在线段AB上时,如题图1所示.由三角形相似(△AQP∽△ABC)关系计算AP的长;
(II)当点P在线段AB的延长线上时,如题图2所示.利用角之间的关系,证明点B为线段AP的中点,从而可以求出AP.
解答 (1)证明:∵PQ⊥AQ,
∴∠AQP=90°=∠ABC,
在△APQ与△ABC中,
∵∠AQP=90°=∠ABC,∠A=∠A,
∴△AQP∽△ABC.
(2)解:在Rt△ABC中,AB=6,BC=8,由勾股定理得:AC=10.
∵∠QBP为钝角,
∴当△PQB为等腰三角形时,
(I)当点P在线段AB上时,如题图1所示.
∵∠QPB为钝角,
∴当△PQB为等腰三角形时,只可能是PB=PQ,
由(1)可知,△AQP∽△ABC,
∴$\frac{PA}{AC}$=$\frac{PQ}{BC}$,即$\frac{6-PB}{10}$=$\frac{PB}{8}$,解得:PB=$\frac{8}{3}$,
∴AP=AB-PB=6-$\frac{8}{3}$=$\frac{10}{3}$;
(II)当点P在线段AB的延长线上时,如题图2所示.
∵∠QBP为钝角,
∴当△PQB为等腰三角形时,只可能是PB=BQ.
∵BP=BQ,∴∠BQP=∠P,
∵∠BQP+∠AQB=90°,∠A+∠P=90°,
∴∠AQB=∠A,
∴BQ=AB,
∴AB=BP,点B为线段AP中点,
∴AP=2AB=2×6=12.
综上所述,当△PQB为等腰三角形时,AP的长为$\frac{10}{3}$或12.
点评 本题考查相似三角形及分类讨论的数学思想,难度不大.第(2)问中,当△PQB为等腰三角形时,有两种情况,需要分类讨论,避免漏解.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
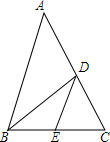 如图,在△ABC中,若$\frac{AB}{AD}$=$\frac{BC}{CD}$,AB=9,BC=6,DE∥AB,则△DCE的面积与四边形ABED的面积比是多少?
如图,在△ABC中,若$\frac{AB}{AD}$=$\frac{BC}{CD}$,AB=9,BC=6,DE∥AB,则△DCE的面积与四边形ABED的面积比是多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
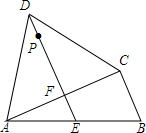 如图,△ABC中,∠ACB=90°,以AC为底边在△ABC外作等腰△ACD,过点D作∠ADC的平分线分别交AB、AC于点E、F.若AC=12cm,BC=5cm,点P是直线DE上的一个动点,则△PBC的周长的最小值是18cm.
如图,△ABC中,∠ACB=90°,以AC为底边在△ABC外作等腰△ACD,过点D作∠ADC的平分线分别交AB、AC于点E、F.若AC=12cm,BC=5cm,点P是直线DE上的一个动点,则△PBC的周长的最小值是18cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
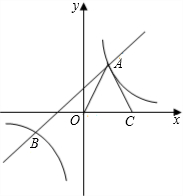 如图,反比例函数${y_1}=\frac{m}{x}$与一次函数y2=kx+b的图象交于两点A(1,3)、B(n,-1).
如图,反比例函数${y_1}=\frac{m}{x}$与一次函数y2=kx+b的图象交于两点A(1,3)、B(n,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
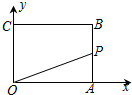 如图,已知矩形OABC,A(4,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动路程为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
如图,已知矩形OABC,A(4,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动路程为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )| A. |  | B. |  | C. | 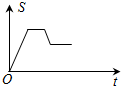 | D. | 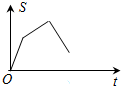 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
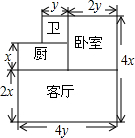 如图是一所住宅的建筑平面图(图中长度单位:m).
如图是一所住宅的建筑平面图(图中长度单位:m).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com