
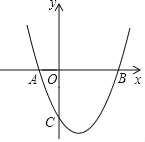
����Ŀ����ͼ����֪������y=ax2+bx��3����A����1��0����B��3��0������M��NΪ�������ϵĶ��㣬����M��MD��y�ᣬ��ֱ��BC�ڵ�D����x���ڵ�E������N��NF��x�ᣬ����Ϊ��F
(1)����κ���y=ax2+bx��3�ı���ʽ��
(2)��M�����������϶Գ����Ҳ�ĵ㣬���ı���MNFEΪ�����Σ���������ε������
(3)��M�����������϶Գ������ĵ㣬�ҡ�DMN=90�㣬MD=MN����ֱ��д����M�ĺ����꣮
���𰸡�(1) y=x2��2x��3�� (2) �����ε����Ϊ24+8![]() ��24��8
��24��8![]() �� (3) ��M�ĺ�����Ϊ��1��
�� (3) ��M�ĺ�����Ϊ��1��![]() ��
��
��������
��1����A����1��0����B��3��0��������������y=ax2+bx��3�����ô���ϵ����������ö��κ���y=ax2+bx��3�ı���ʽ����2�����M������Ϊ��m��m2��2m��3������m��1���ֱ��ʾ��ME=|��m2+2m��3|��MN=2m��2�����ı���MNFEΪ������֪ME=MN���ݴ��г����̣������������ɵ�m��ֵ��������������ε��������3�������ô���ϵ�������ֱ��BC�Ľ���ʽ�����M������Ϊ��t��t2��2t��3������t��1�����N��2��t��t2��2t��3������D��t��t��3������MD=MN�г����̣����ݵ�M��λ�÷����������ɵã�
(1)��A����1��0����B��3��0������y=ax2+bx��3��
�ã�![]() ��
��
���![]() ��
��
�ʸ������߽���ʽΪ��y=x2��2x��3��
(2)��(1)֪�������߽���ʽΪ��y=x2��2x��3=��x��1��2��4��
��������ߵĶԳ�����x=1����������Ϊ��1����4����
��ͼ�����M����Ϊ��m��m2��2m��3��������m��1��
��ME=|��m2+2m+3|��
��M��N����x=1�Գƣ��ҵ�M�ڶԳ����Ҳ࣬
���N�ĺ�����Ϊ2��m��
��MN=2m��2��
���ı���MNFEΪ�����Σ�
��ME=MN��
��|��m2+2m+3|=2m��2��
�����������
�ٵ���m2+2m+3=2m��2ʱ����ã�m1=![]() ��m2=��
��m2=��![]() �����������⣬��ȥ����
�����������⣬��ȥ����
��m=![]() ʱ�������ε����Ϊ��2
ʱ�������ε����Ϊ��2![]() ��2��2=24��8
��2��2=24��8![]() ��
��
�ڵ���m2+2m+3=2��2mʱ����ã�m3=2+![]() ��m4=2��
��m4=2��![]() �����������⣬��ȥ����
�����������⣬��ȥ����
��m=2+![]() ʱ�������ε����Ϊ[2��2+
ʱ�������ε����Ϊ[2��2+![]() ����2]2=24+8
����2]2=24+8![]() ��
��
���������������ε����Ϊ24+8![]() ��24��8
��24��8![]() ��
��
(3)��BC����ֱ�߽���ʽΪy=px+q��
�ѵ�B��3��0����C��0����3���������ʽ��
�ã�![]() ����ã�
����ã�![]() ��
��
��ֱ��BC�ĺ�������ʽΪy=x��3��
���M��������t��t2��2t��3��������t��1��
���N��2��t��t2��2t��3������D��t��t��3����
��MN=2��t��t=2��2t��MD=|t2��2t��3��t+3|=|t2��3t|��
��MD=MN��
��|t2��3t|=2��2t��
�����������
�ٵ�t2��3t=2��2tʱ�����t1=��1��t2=2�����������⣬��ȥ����
�ڵ�3t��t2=2��2tʱ�����t3=![]() ��t2=
��t2=![]() �����������⣬��ȥ����
�����������⣬��ȥ����
������������M�ĺ�����Ϊ��1��![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵxOy�У���ͼ����������y=ax2-4��x��ĸ������ཻ�ڵ�A����y���ཻ�ڵ�B��AB=2![]() .��P���������ϣ��߶�AP��y��������ύ�ڵ�C���߶�BP��x���ཻ�ڵ�D�����P�ĺ�����Ϊm.
.��P���������ϣ��߶�AP��y��������ύ�ڵ�C���߶�BP��x���ཻ�ڵ�D�����P�ĺ�����Ϊm.
��1�������������ߵĽ���ʽ��
��2���ú�m�Ĵ���ʽ��ʾ�߶�CO�ij���
��3����tan��ODC=![]() ʱ�����PAD������ֵ.
ʱ�����PAD������ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+c(a��0)��ͼ���㣨0��1�����ҵ�x=2ʱ�����������ֵΪ4��
��1����������ʽ
��2��ֱ��д������xȡ��ֵʱ������ֵ����1
��3��д��������ͼ������ƽ��1����λ������ƽ��2����λ�����õ��ĺ�������ʽ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ɱ߳�Ϊ1����λ���ȵ�С��������ɵ������߶�AB�Ķ˵��ڸ����.
��1���뽨���ʵ���ƽ��ֱ������ϵxOy��ʹ��A�������Ϊ��-3��-1�����ڴ�����ϵ�£�B�������Ϊ________________��
��2�����߶�BA�Ƶ�B��ʱ����ת90����߶�BC������BC���ڵ�(1)�������ϵ�£�C�������Ϊ__________________��
��3���ڵ�(1)�������ϵ�£����κ���y=ax2+bx+c(a�٣�)��ͼ���O��B��C���㣬��˺���ͼ��ĶԳ��᷽����________________.
���𰸡� ��-1��2�� ��2��0�� x=1
��������������![]() ���ݵ�
���ݵ�![]() �����꽨������ϵ������д����
�����꽨������ϵ������д����![]() ������.
������.
![]() ������
������![]() ��ת��Ķ�Ӧ��
��ת��Ķ�Ӧ��![]() ����
����![]() ,���
,���![]() ������.
������.
![]() �ô���ϵ���������������ʽ����������Գ��᷽��.
�ô���ϵ���������������ʽ����������Գ��᷽��.
��⣺��1����������ϵ��ͼ��
B�������Ϊ![]() ��
��
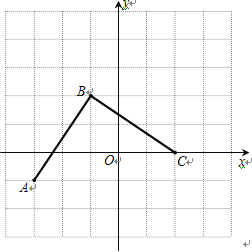
��2���߶�BC��ͼ��C�������Ϊ![]()
��3���ѵ�![]() ������κ���
��������![]() ����
����

��ã�
�����������![]()
�Գ��᷽��Ϊ��![]()
�ʶԳ��᷽����![]()
�㾦������ͼ�������ꣻ��ת���ԳƱ任������ϵ��������κ�������ʽ�����κ�����ͼ��������.�������ո���֪ʶ���ǽ���Ĺؼ�.
�����͡������
��������
18
����Ŀ��������λ���˷������㡪�����������λ����ʮλ������ͬ����λ�������Ϊ10����ô����˵����������λ���ij˻�.�����������λ���ֱ�д��AB��AC����ʮλ����ΪA����λ���ֱַ�ΪB��C��B+C=10��A>3������ô���ǵij˻���һ��4λ����ǰ��λ������A��(A+1)�ij˻�������λ���־���B��C�ij˻�.
�磺47��43=2021��61��69=4209.
��1������ֱ��д��83��87��ֵ��
��2������������λ����ʮλ����Ϊx(
��3��99991��99999=___________________��ֱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij·�ڵ����ˣ�����ֱ�У�Ҳ������ջ��ҹգ����������ֿ�������ͬ���������˾�����·�ڣ��������¼��ĸ��ʣ�
(1)�����˶�������ĸ������� ����ǡ����һ��ֱ�У���һ����յĸ������� ����
(2)�����б�������״ͼ�����������һ��ֱ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����з���������ͬ��������AA1��BB1��CC1��С�������ѡ������һ���ᣬС�����Ҳ�ѡ������һ���ᣬ�������������������һ�������ĸ���Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ƽ���ڣ���![]() ��������
��������![]() ����
����![]() �ڵ�
�ڵ�![]() ����������
����������![]() ����λ�����ѵ�
����λ�����ѵ�![]() ����ƽ��
����ƽ��![]() ����λ������ƽ��
����λ������ƽ��![]() ����λ�õ���
����λ�õ���![]() ��
��
![]() ����ͼ�л���ƽ��ֱ������ϵ��
����ͼ�л���ƽ��ֱ������ϵ��![]() ��д����
�����![]() ����
����![]() �����ꣻ
�����ꣻ
![]() ��ͼ������
��ͼ������![]() ����
����![]() �����Գ�ͼ��
�����Գ�ͼ��![]() ��
��
![]() ���
���![]() �����
�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ȫ���������У�����ij��λȫ��ְ��������ĩ��Ϣʱ��μ���ṫ��������ȫ��ְ���μӹ�����ʱ��![]() ��λ����
��λ����![]() �����˵���ͳ�ƣ����ݵ�������������ͼ��ʾ��������������ͳ��ͼ��������Ϣ�ش��������⣺
�����˵���ͳ�ƣ����ݵ�������������ͼ��ʾ��������������ͳ��ͼ��������Ϣ�ش��������⣺
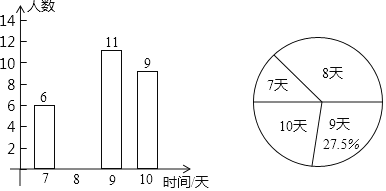
![]() �õ�λְ������______����
�õ�λְ������______����
![]() ��ȫ����ͳ��ͼ��
��ȫ����ͳ��ͼ��
![]() ְ���μӹ���ʱ���������______�죬��λ����______�죻
ְ���μӹ���ʱ���������______�죬��λ����______�죻
![]() ְ���μӹ���ʱ���ܼƴﵽ�����죿
ְ���μӹ���ʱ���ܼƴﵽ�����죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
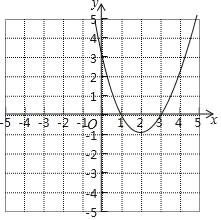
����Ŀ����ƽ��ֱ������ϵxOy�У����κ���y=ax2+bx+c��ͼ����ͼ��ʾ��
��1������κ����ı���ʽ��
��2������ͼ����������P��x1��y����Q��x2��y����������x1��x2����Ϻ���ͼ��ش����⣻
�ٵ�y=3ʱ��ֱ��д��x2��x1��ֵ��
�ڵ�2��x2��x1��3����y��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com