
【题目】如图,在△ABC中,AB=AC=2,BC=![]() ,且∠BAC=120°,点D是线段BC上的一动点(不与点B、C重合),连接AD,作∠ADE=30°,DE交AC于点E.
,且∠BAC=120°,点D是线段BC上的一动点(不与点B、C重合),连接AD,作∠ADE=30°,DE交AC于点E.
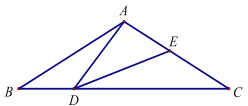
(1)求证:∠BAD∠EDC;
(2)当BD= 时,△ABD≌△EDC,并说明理由.
(3)当△ADE是直角三角形时,求AD的长?
【答案】(1)证明见解析;(2)答案见解析;(3)![]() 或1
或1
【解析】
(1)根据等腰三角形的性质及三角形内角和定理得出∠B=30°,然后根据三角形外角的性质即可得出结论;
(2)先求出DC的长,可得到AB=DC.根据ASA即可证明△ABD≌△EDC;
(3)分两种情况讨论:①当∠DAE=90°时,△CAD是含30°角的直角三角形,可得出AC=![]() AD=2,求出AD的长即可.
AD=2,求出AD的长即可.
②当∠DEA=90°时,∠DAE=∠BAD=60°,得到△ABD是含30°角的直角三角形,即可得到AD的长.
(1)∵∠BAC=120°,AB=AC,∴∠B=∠C=30°.
又∵∠ADC=∠B+∠BAD,∴∠ADE+∠EDC=∠B+∠BAD.
又∵∠ADE=30°,∴∠BAD=∠EDC.
(2)当BD=![]() 时,△ABD≌△EDC.理由如下:
时,△ABD≌△EDC.理由如下:
∵BD=![]() ,BC=
,BC=![]() ,∴DC=
,∴DC=![]() =2,∴AB=DC.
=2,∴AB=DC.
在△ABD和△EDC中,∵∠B=∠C,AB=DC,∠BAD=∠EDC,∴△ABD≌△EDC.
(3)①当∠DAE=90°时.
∵∠C=30°,∴AC=![]() AD=2,∴AD=
AD=2,∴AD=![]() =
=![]() .
.
②当∠DEA=90°时,∠DAE=∠BAD=60°.
又∵∠B=30°,∴∠ADB=90°,∴AD=![]() AB=1.
AB=1.
综上所述:当△ADE 是直角三角形时,AD=![]() 或1.
或1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,正比例函数 ![]() 的图象与反比例函数
的图象与反比例函数 ![]()
![]() 在第一象限的图象交于点
在第一象限的图象交于点 ![]() ,过点
,过点 ![]() 作
作 ![]() 轴的垂线,垂足为
轴的垂线,垂足为 ![]() ,已知△OAM的面积为1.
,已知△OAM的面积为1.
(1)求反比例函数的解析式;
(2)如果点 ![]() 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点 ![]() 与点
与点 ![]() 不重合),且点
不重合),且点 ![]() 的横坐标为1,在
的横坐标为1,在 ![]() 轴上求一点
轴上求一点 ![]() ,使
,使 ![]() 最小.
最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)﹣![]() ﹣(+13)+(﹣
﹣(+13)+(﹣![]() )﹣(﹣17)
)﹣(﹣17)
(2)﹣22+3÷(﹣1)2017﹣|﹣4|×5
(3)先化简再求值﹣3(2x2﹣xy)+4(x2+xy﹣6),其中x=﹣1,y=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空:
(1)(-5a4)·(-8ab2)=___.
(2)3x2y·![]() ·(5xy2)=___.
·(5xy2)=___.
(3)![]() (2x-3y)=___.
(2x-3y)=___.
(4)(-2ab)·(3a2-2ab-4b2)=___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,AD⊥BC,垂足为点 D.下列说法中:①∠B的余角只有∠BAD;②∠B=∠C;③线段 AB 的长度表示点 B 到直线 AC 的距离;④AB·AC=BC·AD;一定正确的有( )
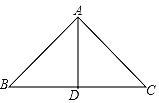
A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于![]() 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)3x3x9﹣2xx3x8
(2)﹣12+20160+(![]() )2017×(﹣4)2018
)2017×(﹣4)2018
(3)(x+4)(x﹣4)﹣(x﹣2)2
(4)ab(a+b)﹣(a﹣b)(a2+b2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期学习了分式方程的解法,下面是晶晶同学的解题过程:
解方程 ![]()
解:整理,得: ![]() …………………………第①步
…………………………第①步
去分母,得: ![]() …………………………第②步
…………………………第②步
移项,得: ![]() ……………………… 第③步
……………………… 第③步
合并同类项,得: ![]() ……………………… 第④步
……………………… 第④步
系数化1,得: ![]() …………………………第⑤步
…………………………第⑤步
检验:当![]() 时,
时,![]()
所以原方程的解是![]() . ………………………第⑥步
. ………………………第⑥步
上述晶晶的解题过程从第_____步开始出现错误,错误的原因是_________________.请你帮晶晶改正错误,写出完整的解题过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com