Question

15．如图，在圆内接四边形ABCD中，若∠ADB=∠ABC，点P为对角线BD上的一点，已知BD=6，CD=4．
（1）当BP为多少时，△APD是以PD为底的等腰三角形？
（2）在（1）的条件下，若cos∠ACB=$\frac{{\sqrt{5}}}{5}$，求AB的长．

Answer 1

分析 （1）先写出BD的值等于多少，再根据BD的值和已知条件说明△APD是以PD为底的等腰三角形即可；
（2）作AE⊥BD于点E，然后根据等腰三角形的性质，可知AE为△APD的中线，然后根据第一问可以求得DE的长，从而可以求得AD、AE的长，进而可以求得AB的长．

解答 解：（1）当BP=4时，△APD是以PD为底的等腰三角形．
理由：∵在⊙O中，
∴∠ABP=∠ACD，∠ADB=∠ACB，
∵∠ADB=∠ABC，
∴∠ABC=∠ACB，
∴AC=AB，
∵CD=4，BP=4，
∴CD=BP，
在△ABP和△ACD中，
$\left\{\begin{array}{l}{AB=AC}\\{∠ABP=∠ACD}\\{BP=CD}\end{array}\right.$，
∴△ABP≌△ACD（SAS）
∴AP=AD，
即当BP=4时，△APD是以PD为底的等腰三角形．
（2）作AE⊥BD于点E，如下图所示，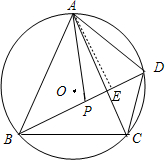

∵BP=4，BD=6，△APD是等腰三角形，AE⊥BD，
∴DP=2，DE=$\frac{1}{2}×PD=1$，BE=5，
∵cos∠ACB=$\frac{{\sqrt{5}}}{5}$，∠ACB=∠ADE，
∴cos∠ADE=$\frac{\sqrt{5}}{5}$，
∵cos∠ADE=$\frac{DE}{AD}$，
∴AD=$\sqrt{5}$，
∴AE=$\sqrt{A{D}^{2}-D{E}^{2}}=\sqrt{（\sqrt{5}）^{2}-{1}^{2}}=2$，
∴AB=$\sqrt{B{E}^{2}+A{E}^{2}}=\sqrt{{5}^{2}+{2}^{2}}=\sqrt{29}$，
即AB的长是$\sqrt{29}$．

点评 本题考查相似三角形的判定和性质、圆周角定理和等腰三角形的性质、锐角三角函数值，解题的关键是明确题意，找出所求问题需要的条件．