
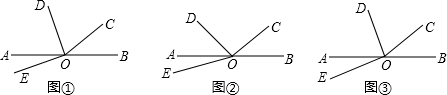
分析 (1)由∠BOC=α=40°,根据邻补角的定义可得∠AOC=140°,再利用角平分线的定义,由OD平分∠AOC,可得∠AOD=$\frac{1}{2}$∠AOC=70°,即可得到∠AOE=∠DOE-∠AOD=20°;
(2)由∠BOC=α,根据邻补角的定义可得∠AOC=180°-α,因为∠AOD=$\frac{1}{3}$∠AOC,所以∠AOD=$\frac{1}{3}$(180°-α)=60°-$\frac{1}{3}$α,再利用角的和差关系得到∠AOE=∠DOE-∠AOD=60°-(60°-$\frac{1}{3}$α)=$\frac{1}{3}$α;
(3)由∠BOC=α,根据邻补角的定义可得∠AOC=180°-α,因为∠AOD=$\frac{1}{n}$∠AOC,利用等量代换可得∠AOD=$\frac{1}{n}$(180°-α)=$\frac{180°}{n}$-$\frac{α}{n}$,根据角的和差关系即可得到∠AOE=∠DOE-∠AOD=$\frac{180°}{n}$-($\frac{180°}{n}$-$\frac{α}{n}$)=$\frac{α}{n}$.
解答 解:(1)∵∠BOC=α=40°,
∴∠AOC=140°,
∵OD平分∠AOC,
∴∠AOD=$\frac{1}{2}$∠AOC=70°,
∵∠DOE=90°,
∴∠AOE=∠DOE-∠AOD=20°;
(2)∵∠BOC=α,
∴∠AOC=180°-α,
∵∠AOD=$\frac{1}{3}$∠AOC,
∴∠AOD=$\frac{1}{3}$(180°-α)=60°-$\frac{1}{3}$α,
∵∠DOE=60°,
∴∠AOE=∠DOE-∠AOD=60°-(60°-$\frac{1}{3}$α)=$\frac{1}{3}$α;
(3)∠AOE与∠BOC的数量关系为:∠AOE=$\frac{α}{n}$.
点评 本题主要考查了角平分线的定义,角的和差关系,得到角之间的和差关系是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | |c|=$\frac{1}{2}$|b| | B. | |c|=$\frac{1}{3}$|b| | C. | |c|=$\frac{1}{4}$|b| | D. | |c|=$\frac{3}{4}$|b| |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
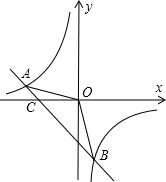 如图,已知点A(一8,n),B(3,-8)是一次函数y=kx+b的图象和反比例函数$y=\frac{m}{x}$图象的两个交点.
如图,已知点A(一8,n),B(3,-8)是一次函数y=kx+b的图象和反比例函数$y=\frac{m}{x}$图象的两个交点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
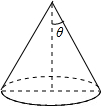 如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是( )
如图,已知圆锥的底面半径为5,侧面积为65π,设圆锥的母线与高的夹角为θ,则cosθ的值是( )| A. | $\frac{5}{12}$ | B. | $\frac{5}{13}$ | C. | $\frac{10}{13}$ | D. | $\frac{12}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com