
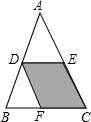
 如图,在△ABC中,D、E分别是边AB、AC的中点,连接DE,将△ADE沿AB方向平移到△DBF的位置,点D在BC上,已知△ADE的面积为1,则四边形CEDF的面积是2.
如图,在△ABC中,D、E分别是边AB、AC的中点,连接DE,将△ADE沿AB方向平移到△DBF的位置,点D在BC上,已知△ADE的面积为1,则四边形CEDF的面积是2. 分析 由题可知△ADE∽△ABC相似且相似比是1:2,根据相似比求面积比;然后再由平移的性质来求四边形CEDF的面积:S四边形CEDF=S四边形DBCE-S△ADE.
解答  解:∵如图,将△ADE沿AB方向平移到△DBF的位置,点D在BC上,△ADE的面积为1,
解:∵如图,将△ADE沿AB方向平移到△DBF的位置,点D在BC上,△ADE的面积为1,
∴S△DBF=S△ADE=1.
∵D,E分别是AB,AC的中点,
∴DE∥BC,
∴△ADE∽△ABC,
∴$\frac{S△ADE}{{S}_{△ABC}}$=($\frac{AD}{AB}$)2,即$\frac{1}{{S}_{△ABC}}$=($\frac{1}{2}$)2=$\frac{1}{4}$,
故S△ABC=4,
∴S四边形DBCE=3,
∴S四边形CEDF=S四边形DBCE-S△ADE=3-1=2.
故答案是:2.
点评 本题考查平移的性质和相似三角形的判定与性质,此题利用相似三角形面积的比等于相似比的平方求得S四边形DBCE=3是解题的难点.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
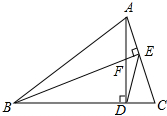 如图,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F,连接DE.
如图,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $1÷6×\frac{1}{6}=\frac{1}{36}$ | B. | (-2)-2=4 | C. | $\frac{1}{3}-2-(-2\frac{1}{3})=\frac{2}{3}$ | D. | 20150=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 13.5万元 | B. | 45万元 | C. | 54万元 | D. | 100万元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com