

分析 (1)证△EAF≌△CAF,推出EF=CF,∠E=∠ACF,根据等腰三角形性质推出∠E=∠ABE,即可得出答案;
(2)在FB上截取BM=CF,连接AM,证△ABM≌△ACF,推出EF=FC=BM,AF=AM,推出△AMF是等边三角形,推出MF=AF,即可得出答案;
(3)①在FB上截取BM=CF,连接AM,证△ABM≌△ACF,推出EF=FC=BM,AF=AM,推出△AMF是等腰直角三角形,推出MF=$\sqrt{2}$AF,即可得出答案;
②只需在CF上截取CG=BF,先证△AFE≌△AFC,得出CF=EF,再证△ABF≌△ACG,得出△AFG是等腰直角三角形,然后结论显然.
解答 证明:(1)如图1,
∵AF平分∠CAE,
∴∠EAF=∠CAF,
∵AB=AC,AB=AE,
∴AE=AC,
在△ACF和△AEF中,
$\left\{\begin{array}{l}{AE=AC}\\{∠EAF=∠CAF}\\{AF=AF}\end{array}\right.$,
∴△ACF≌△AEF(SAS),
∴∠E=∠ACF,
∵AB=AE,
∴∠E=∠ABE,
∴∠ABE=∠ACF;
(2)在FB上截取BM=CF,连接AM,如图2,
∵△ACF≌△AEF,
∴EF=CF,∠E=∠ACF=∠ABM,
在△ABM和△ACF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABM=∠ACF}\\{BM=CF}\end{array}\right.$,
∴△ABM≌△ACF(SAS),
∴AM=AF,∠BAM=∠CAF,
∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠BAC=60°,
∴∠MAF=∠MAC+∠CAF=∠MAC+∠BAM=∠BAC=60°,
∵AM=AF,
∴△AMF为等边三角形,
∴AF=AM=MF,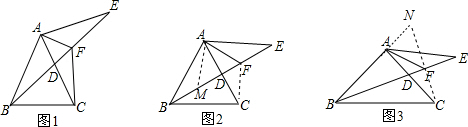
∴AF+EF=BM+MF=FB,
即AF+EF=FB;
(3)①线段AF、EF、FB不是(2)中的结论,线段AF、EF、FB的数量关系为$\sqrt{2}$AF+EF=FB,理由如下:
在FB上截取BM=CF,连接AM,如图3,
∵△ACF≌△AEF,
∴EF=CF=BM,∠E=∠ACF=∠ABM,
在△ABM和△ACF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABM=∠ACF}\\{BM=CF}\end{array}\right.$,
∴△ABM≌△ACF(SAS),
∴AM=AF,∠BAM=∠CAF,
∵AB=AC,∠ABC=45°,
∴△ABC是等腰直角三角形,
∴∠BAC=90°,
∴∠MAF=∠MAC+∠CAF=∠MAC+∠BAM=∠BAC=90°,
∵AM=AF,
∴△AMF为等腰直角三角形,
∴MF=$\sqrt{2}$AF,
∴FB=BM+MF=EF+$\sqrt{2}$AF,
即$\sqrt{2}$AF+EF=FB;
②如图4,在CF上截取CG=BF,连接AG,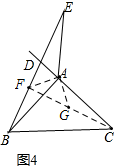
在△AFE和△AFC中,
$\left\{\begin{array}{l}{AF=AF}\\{∠FAE=∠FAC}\\{AE=AC}\end{array}\right.$,
∴△AFE≌△AFC(SAS),
∴FE=FC,∠FEA=∠FCA,
∵AB=AE,
∴∠ABF=∠AEF=∠ACF,
在△ABF和△ACG中,
$\left\{\begin{array}{l}{BF=CG}\\{∠FBA=∠GCA}\\{BA=CA}\end{array}\right.$,
∴△ABF≌△ACG(SAS),
∴AG=AF,∠FAB=∠GAC,
∵AB=AC,∠ABC=45°,
∴∠BAC=90°,
∴FAG=90°,
∴△AFG是等腰直角三角形,
∴FG=$\sqrt{2}$AF,
∵CF=CG+GF,
∴CF=BF+$\sqrt{2}$AF,
∴EF=BF+$\sqrt{2}$AF.
点评 本题主要考查了全等三角形的判定与性质、等腰三角形的性质、等边三角形的判定与性质、角平分线的性质、等腰直角三角形的判定与性质等知识点,难度中等.熟悉各种特殊三角形的性质、全等三角形的判定方法以及正确作出辅助线是解答的关键.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:解答题
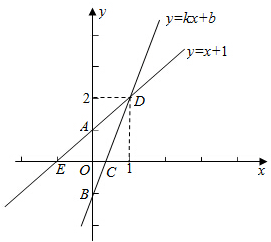 如图,已知直线y=x+1与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),并且与x轴以及直线y=x+1分别交于点C、D.
如图,已知直线y=x+1与y轴交于点A,一次函数y=kx+b的图象经过点B(0,-1),并且与x轴以及直线y=x+1分别交于点C、D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “十字相乘法”能把二次三项式分解因式,对于形如ax2+bxy+cy2的x,y二次三项式来说,方法的关键是把x2项系数a分解成两个因数a1,a2的积,即a=a1•a2,把y2项系数c分解成两个因数,c1,c2的积,即c=c1•c2,并使a1•c2+a2•c1正好等于xy项的系数b,那么可以直接写成结果:ax2+bxy+cy2=(a1x+c1y)(a2x+c2y)
“十字相乘法”能把二次三项式分解因式,对于形如ax2+bxy+cy2的x,y二次三项式来说,方法的关键是把x2项系数a分解成两个因数a1,a2的积,即a=a1•a2,把y2项系数c分解成两个因数,c1,c2的积,即c=c1•c2,并使a1•c2+a2•c1正好等于xy项的系数b,那么可以直接写成结果:ax2+bxy+cy2=(a1x+c1y)(a2x+c2y)
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
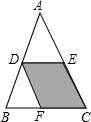 如图,在△ABC中,D、E分别是边AB、AC的中点,连接DE,将△ADE沿AB方向平移到△DBF的位置,点D在BC上,已知△ADE的面积为1,则四边形CEDF的面积是2.
如图,在△ABC中,D、E分别是边AB、AC的中点,连接DE,将△ADE沿AB方向平移到△DBF的位置,点D在BC上,已知△ADE的面积为1,则四边形CEDF的面积是2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com