Question

已知正比例函数y=k₁x的图象与反比例函数y=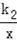的图象的一个交点是（2，3）．

（1）求出这两个函数的表达式；

（2）作出两个函数的草图，利用你所作的图形，猜想并验证这两个函数图象的另一个交点的坐标；

（3）直接写出使反比例函数值大于正比例函数值的x的取值范围．

　

Answer 1

【考点】反比例函数与一次函数的交点问题．

【分析】（1）根据待定系数法，可得函数解析式；

（2）根据函数解析式确定出图象所经过的点的坐标，再画出图象即可．

（3）根据图象和交点坐标即可求得．

【解答】解：（1）由正比例函数y=k₁x的图象与反比例函数y=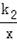的图象的一个交点是（2，3），得

3=2k₁，3=．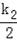

解得k₁=，k₂=6．

正比例函数y=x；反比例函数y=；

（2）画出函数的图象如图：

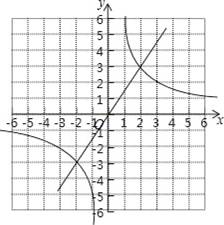
两个函数图象的一个交点的坐标（2，3），猜想另一个交点的坐标（﹣2，﹣3），

把（﹣2，﹣3）代入y=成立；

（3）由图象可知：比例函数值大于正比例函数值的x的取值范围是x＜﹣2或0＜x＜2．

【点评】本题考查了反比例函数与一次函数的交点问题，一次函数和反比例函数的图象，以及函数与不等式的关系，正确画出函数的图象是解题的关键．