练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知扇形的圆心角为45°，半径长为12，用它围成一个圆锥的侧面，那么圆锥的底面半径为（　　）

    A．3       B．1.5    C．2       D．2.5

    　


    B【考点】圆锥的计算．

    【分析】根据扇形的弧长公式求出扇形弧长，即圆锥的底面周长，根据圆的周长公式计算即可．

    【解答】解：∵扇形的圆心角为45°，半径长为12，

    ∴扇形的弧长为： =3π，

    ∴圆锥的底面周长为3π，

    则圆锥的底面比较为1.5．

    故选：B．

    【点评】本题考查的是圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


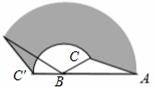
    如图，在△ABC中，AB=4cm，BC=2cm，∠ABC=30°，把△ABC以点B为中心按逆时针方向旋转，使点C旋转到AB边的延长线上的点C′处，那么AC边扫过的图形（图中阴影部分）的面积是　　　　　　cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，梯子（长度不变）跟地面所成的锐角为A，关于∠A的三角函数值与梯子的倾斜程度之间，叙述正确的是（　　）

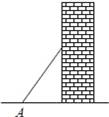
    A．sinA的值越大，梯子越陡     B．cosA的值越大，梯子越陡

    C．tanA的值越小，梯子越陡     D．陡缓程度与∠A的函数值无关

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知正比例函数y=k1x的图象与反比例函数y=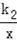的图象的一个交点是（2，3）．

    （1）求出这两个函数的表达式；

    （2）作出两个函数的草图，利用你所作的图形，猜想并验证这两个函数图象的另一个交点的坐标；

    （3）直接写出使反比例函数值大于正比例函数值的x的取值范围．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，D是△ABC的边AB上的一点，那么下列四个条件不能单独判定△ABC∽△ACD的是（　　）

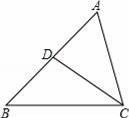
    A．∠B=∠ACD    B．∠ADC=∠ACB       C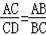．    D．AC2=AD•AB

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在等边△ABC中，AB=6，D是BC的中点，将△ABD绕点A旋转后得到△ACE，那么线段DE的长度为　　　　　　．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


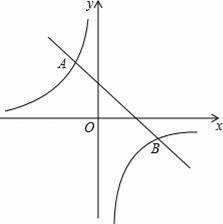
    如图：已知反比例函数y=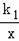与一次函数y=k2x+b的图象交于A（2，﹣1），B（）．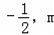

    （1）求k1、k2，b的值；

    （2）求三角形AOB的面积；

    （3）若M（x1，y1），N（x2，y2）是反比例函数y=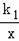图象上的两点，且x1＜x2，y1＞y2，指出M、N各位于哪个象限，并简单说明理由．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    直线y=mx+n与双曲线y=相交于A（﹣1，2），B（2，b）两点，与y轴相交于点C．求m、n的值及y=的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若|x|=|4|，那么x=（　　）

    A．﹣4   B．4       C．4或﹣4    D．不能确定

    　

    查看答案和解析>>

    同步练习册答案