
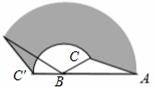
如图,在△ABC中,AB=4cm,BC=2cm,∠ABC=30°,把△ABC以点B为中心按逆时针方向旋转,使点C旋转到AB边的延长线上的点C′处,那么AC边扫过的图形(图中阴影部分)的面积是 cm2.

科目:初中数学 来源: 题型:
如图所示,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两条直角边长都为3,另一种纸片的两条直角边长分别为1和3.图1、图2、图3是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.
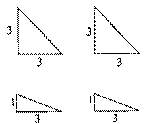



图1 图2 图3
(1)请用三种方法(拼出的两个图形只要不全等就认为是不同的拼法)将图中所给四块直角三角形纸片拼成平行四边形(非矩形),每种方法要把图中所给的四块直角三角形纸片全部用上,互不重叠且不留空隙,并把你所拼得的图形按实际大小画在图1、图2、图3的方格纸上(要求:所画图形各顶点必须与方格纸中的小正方形顶点重合;画图时,要保留四块直角三角形纸片的拼接痕迹);
(2)三种方法所拼得的平行四边形的面积是否是定值?若是定值,请直接写出这个定值;若不是定值,请直接写出三种方法所拼得的平行四边形的面积各是多少;
(3)三种方法所拼得的平行四边形的周长是否是定值?若是定值,请直接写出这个定值;若不是定值,请直接写出三种方法所拼得的平行四边形的周长各是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB为半圆O的直径,C为半圆上一点,且弧AC为半圆的
 ,设扇形AOC,△COB,弓形BmC的面积分别为S1,S2,S3,则下列结论正确的是( )
,设扇形AOC,△COB,弓形BmC的面积分别为S1,S2,S3,则下列结论正确的是( )
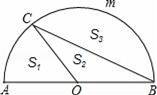

A.S1<S2<S3 B.S2<S1<S3 C.S2<S3<S1 D.S1<S2<S3
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个布袋中装有2个红球和2个篮球,它们除颜色外其他都相同.
(1)搅匀后从中摸出一个球记下颜色,不放回继续再摸第二个球,求两次都摸到红球的概率;
(2)在这4个球中加入x个用一颜色的红球或篮球后,进行如下试验,搅匀后随机摸出1个球记下颜色,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到红球的概率稳定在0.80,请推算加入的是哪种颜色的球以及x的值大约是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com