
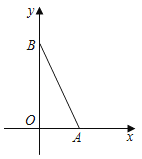
【题目】在平面直角坐标系中,点A(2,0),B(0,4),若以B,O,C为顶点的三角形与△ABO全等,则点C的坐标不能为( )
A.(0,﹣4)B.(﹣2,0)C.(2,4)D.(﹣2,4)
【答案】A
【解析】
根据全等三角形的判定定理画图并逐一判断即可.
解:如图所示:
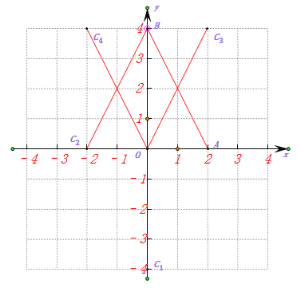
∵A(2,0),B(0,4)
∴OA=2,OB=4,∠AOB=90°
当C1坐标为(0,﹣4)时,B、O、C1同一条直线上,不能构成三角形,故选A;
当C2坐标为(﹣2,0)时,OC2= OA=2,∠C2O B =∠AOB=90°,OB=OB
∴△C2O B≌△AOB,故不选B;
当C3坐标为(2,4)时,BC3= OA=2,∠C3 B O =∠AOB=90°,OB=BO
∴△C3BO≌△AOB,故不选C;
当C4坐标为(﹣2,4)时,BC4= OA=2,∠C4BO =∠AOB=90°,OB=BO
∴△C4BO≌△AOB,故不选D.
故选A.


科目:初中数学 来源: 题型:
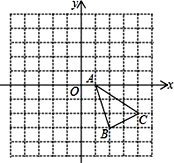
【题目】如图,平面直角坐标系中,△ABC三个顶点的坐标分别为A(1,0),B(2,-3),C(4,-2).
(1)在图中作出△ABC关于x轴对称的图形△A1B1C1.
(2)作出△A1B1C1向左平移4个单位长度后得到的△A2B2C2,并直接写出点C2的坐标_____.
(3)△A2B2C2的面积是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究.
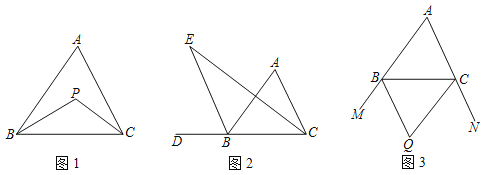
(1)如图1,在△ABC中,∠ABC与∠ACB的平分线交于点P,∠A=64°,则∠BPC= ;
(2)如图2,△ABC的内角∠ACB的平分线与△ABC的外角∠ABD的平分线交于点E.其中∠A=α,求∠BEC.(用α表示∠BEC);
(3)如图3,∠CBM、∠BCN为△ABC的外角,∠CBM、∠BCN的平分线交于点Q,请你写出∠BQC与∠A的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
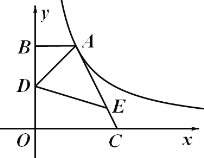
【题目】如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,
点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE
的面积为3,则k的值为 ▲ .
查看答案和解析>>
科目:初中数学 来源: 题型:
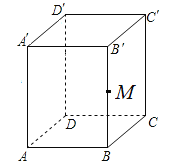
【题目】如图,长方体ABCD-A'B'C'D'是个无上底长方体容器,长AB=5cm,宽BC=3cm,高AA′=8cm,甜食点M在容器内侧,位于侧棱BB′的中点,一只蚂蚁从容器外部的A爬到点M处吃甜食,这只蚂蚁爬行的最短路径是( )cm
A.![]() B.13C.
B.13C.![]() D.14
D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=90°![]() ∠A
∠A
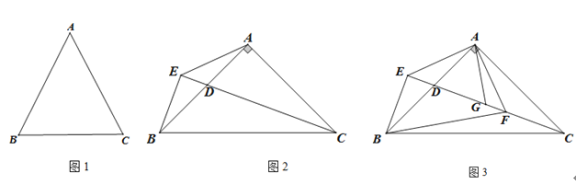
(1)如图1,求证:AB=AC;
(2)如图2,若∠BAC=90°,点D为AB上一点,过点B作直线CD的垂线,垂足为E,连接AE, 求∠AEC的度数;
(3)如图3,在(2)的条件下,过点A作AE的垂线交CE于点F,连接BF,若∠ABF-∠EAB=15°,G为DF上一点,连接AG,若∠AGD=∠EBF,AG=6,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC 是等边三角形,点 P 在△ABC 内,PA=2,将△PAB 绕点 A 逆时针旋转得到△P1AC,则 P1P 的长等于( )

A. 2 B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com